你好，我是胡光。上次课里关于判断和循环的内容你做练习了么？其实这两部分内容都不复杂，你想，判断就是“如果…就…”，而循环就是重复做一件事情。程序里，只是我们换了一种方式来描述和抽象这两个场景。 ## 今日任务 今天的任务其实也是和上次讲的内容有很大关系。如果你对上次讲的内容不理解，我建议你先再好好回顾下上次讲的知识，然后开始今天的任务。 先来看看今天这 10 分钟我们要完成的任务。圆周率 π 对你来说肯定不是一个陌生的概念，它指的是圆的周长与直径的比值。在古代，数学家们为了计算 π 的精确值想尽方法，可能穷尽一生也不过精确到小数点后几位而已。但到了现在，你可能不相信，只要你知道 π 的定义，就可以利用编程轻易计算出 π 的值。那究竟怎么做到呢？ 我们先来看一个用蒙特卡罗法计算 π 的示意图：
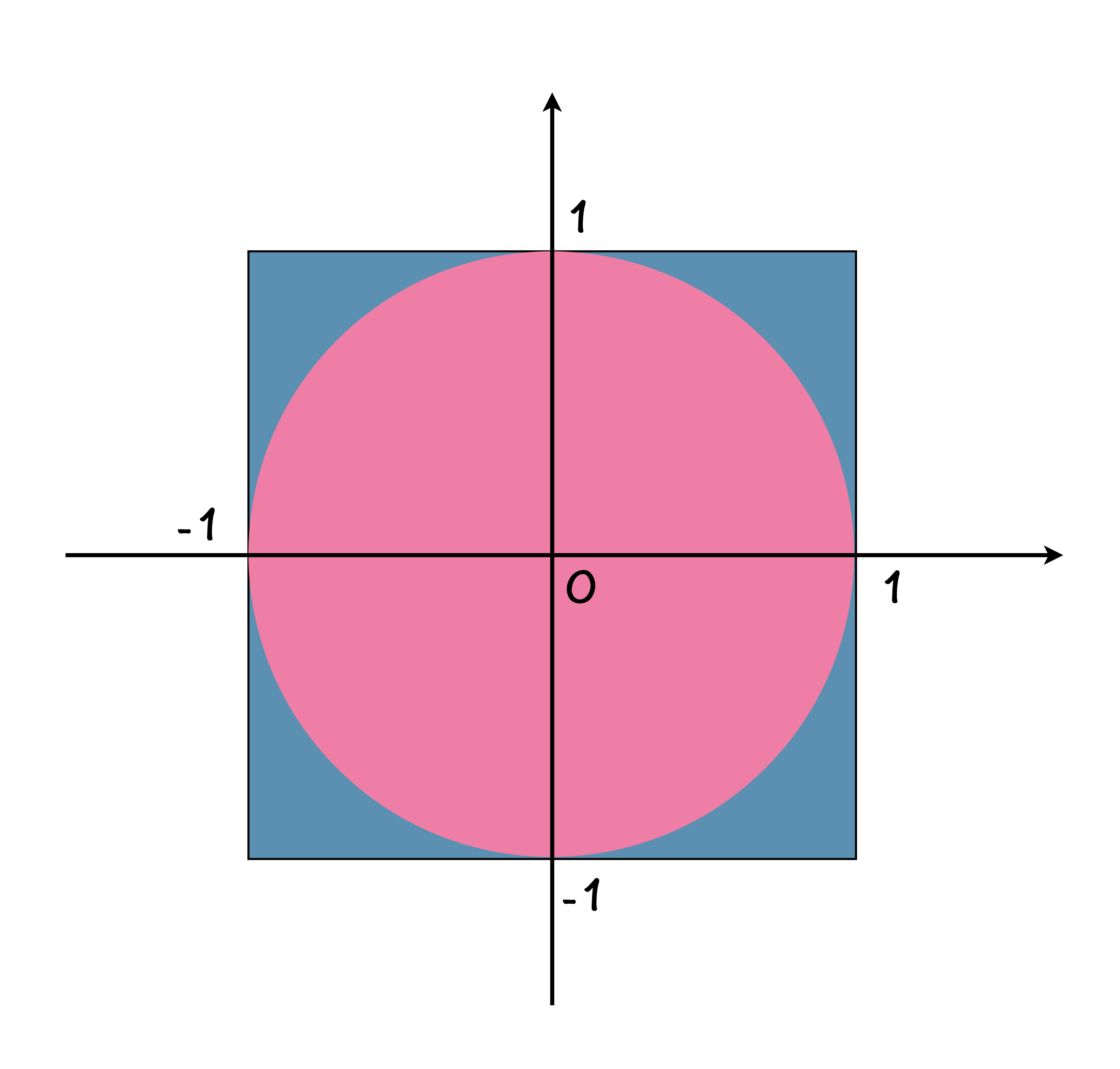
通过观察图1，请你思考一个问题，如果你随机地在正方形区域中选择一个点，那么这个被选择的点，也恰巧落在圆形红色区域的概率是多大？这个问题很简单，就是圆面积和正方形面积的比值，简单计算就可以得到这个概率值，应该是 π/4。 也就是说，如果我们做大量的随机实验，最终落在圆内部的次数除以总次数再乘以 4 得到的值，应该接近圆周率 π。随机次数越多，所得到的数值越接近 π。你肯定不喜欢做这种重复的“重体力”劳动，但如果你写好编程，让它帮你做这件事，那就简单容易快捷多了。计算机可是一个不怕辛苦、没有怨言的好帮手，今天就让它来帮助我们完成这个任务吧。 ## 必知必会，查缺补漏 思考一下，其实要完成上面这个任务，我们已经具备了一些基础知识，比如说：分支结构（if…else）可以帮助你判断某个点是否在圆内部，循环结构（for/while）可以帮助你完成大量的重复实验。 说到这里，你会发现，面对今天的这个任务，我们还需要做到随机选点，那么这个随机操作，在计算机中应该如何来完成呢？今天我将告诉你的就是程序语言中的随机函数，准备好了么？让我们开始吧。 #### 1.真随机与伪随机 说到随机，就需要说一下真随机与伪随机的概念了。 所谓**真随机**其实并不难理解，我们以掷骰子为例，掷出 1～6 点的概率均为 1/6，如果我问你，上一次掷出的点数是4，那么下一次掷出 6 点的概率是多大？你会发现，依然是 1/6，我们称这两次掷骰子的事件是相互独立的，上一次的结果和下一次之间没有必然联系。

通过上面这个示意图，你就很容易看出，所谓真随机，就是我们通常意义下的随机。那么什么又是伪随机呢？从名字上面来看，伪随机，带个伪字，说明本质上不是随机，可看起来是随机。 下面请你注意观察下图的两个数字循环序列：
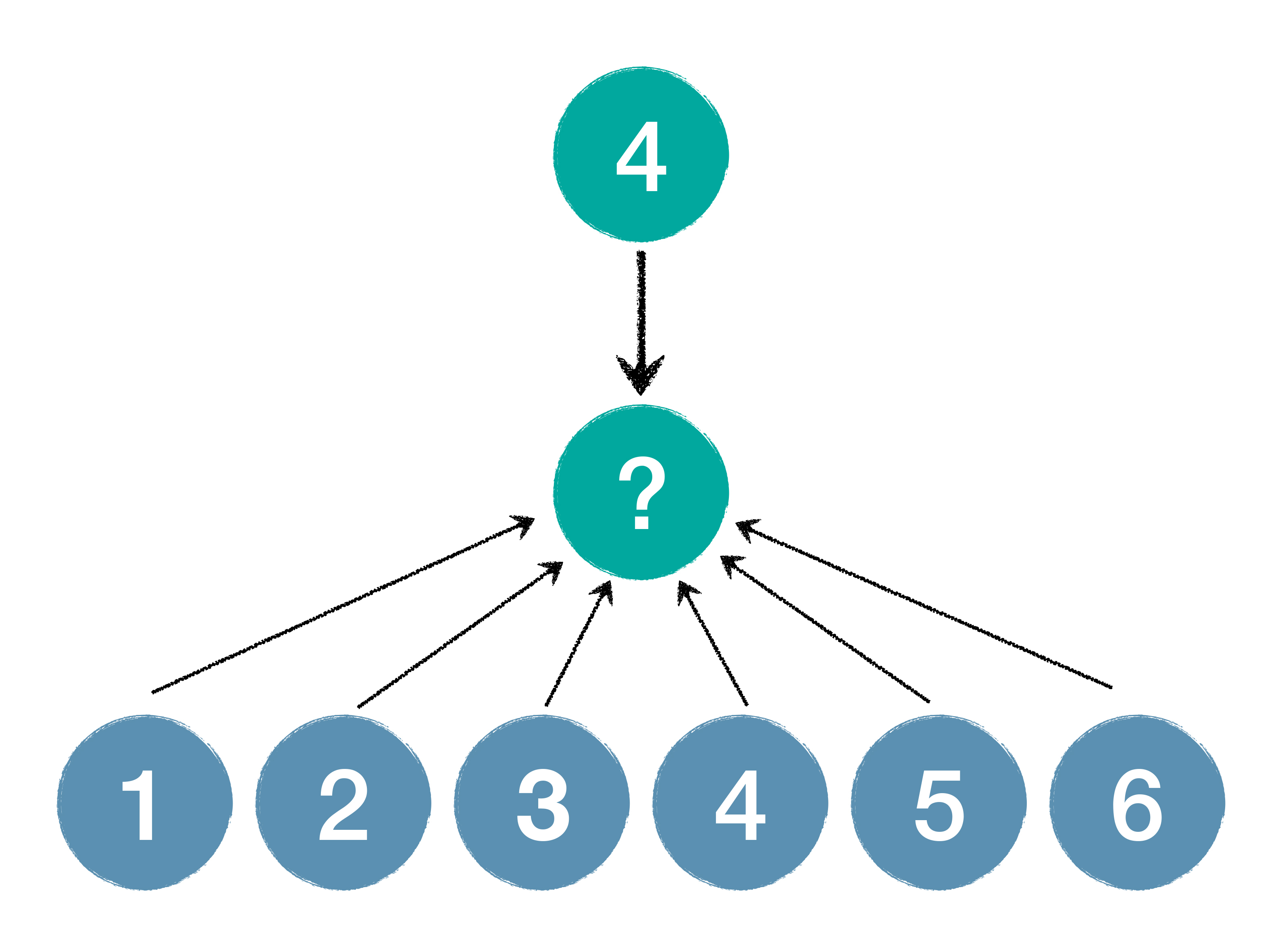
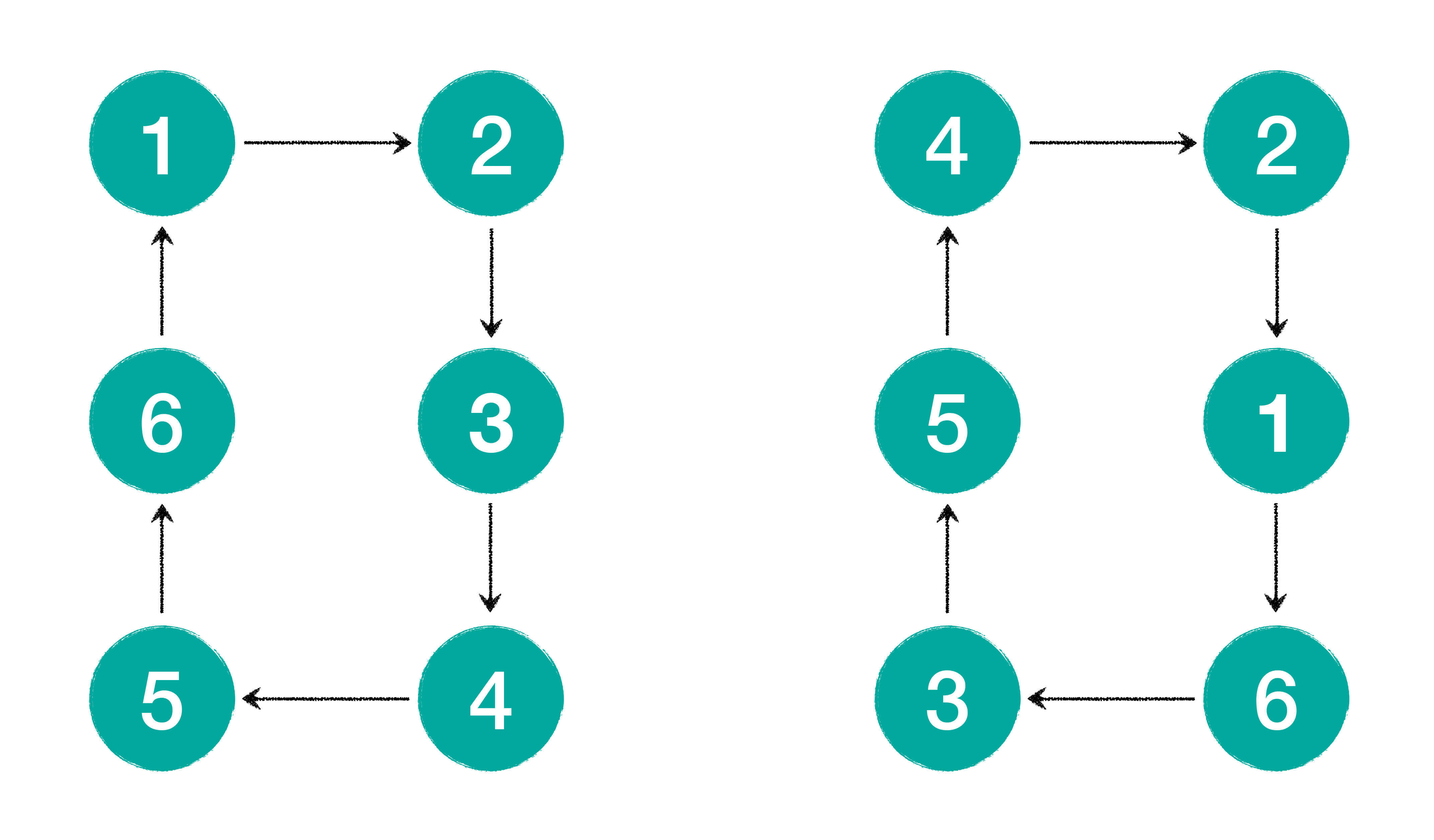你观察上面这两个数字序列，会发现，第一个序列是123456，这是一个有明显规律的序列，你一定不会觉得这个序列是随机生成的。另一个序列是421635，好像没有什么明显的规律，相比于第一个序列，你是不是更偏向于相信第二个序列是随机生成的序列呢？ 第二个序列就是我刚刚所说的伪随机，看起来像是随机序列，可实际上，4后面一定会出现2，2后面一定是1，1后面一定是6，也就是说前一个数字决定了后一个数字。 计算机中究竟如何制造出来这样一个伪随机序列呢，这个问题留到后面的 “动手搞事情” 中，我会使用一行简单的数学公式，制造一个包含100个数字的伪随机数字序列，类似于上图中第二个序列的加大版。 最后你会发现，**所谓计算机中的伪随机数序列**，**就是类似第二个序列那样的，没有什么明显规律的一个规模更大的循环序列。** 现在你知道为什么叫做伪随机了吧，那是因为，一旦要是上一个随机函数的值确定了，下一个数字也就确定了，而纯正意义上的真随机，应该是前后两次出现的数字是两次独立事件，没有任何关系。 #### 2.程序中的随机函数 现在我们所接触到的语言中，没有真随机，全是伪随机。也就是说，语言中给我们准备好了一个随机函数，这个随机函数会根据上一个**随机值**和一个**固定的计算规则**，得到下一个**随机值**。 而你在其他资料中可能会看到**随机种子**这个概念，设置随机种子就是在设置随机函数中记录的上一个随机值。例如，上面我们自己做出来的6个长度的伪随机序列，如果随机种子设置为值1，我们得到的值依次是 635421，如果设置为值 3，那么我们将依次得到 542163。 下面就看看 C 语言中的随机函数的用法吧： ``` #include <stdio.h> #include <stdlib.h> #include <time.h> int main() { printf("%d\n", rand() % 1000); // 永远输出固定值 srand(time(0)); printf("%d\n", rand() % 1000); // 每次运行都不同 return 0; } ``` 上面代码中，我们用 rand() 函数，获得一个随机值，这个就是我们前面讲的随机函数，它将依次的返回随机序列中的每一个值。 而 srand() 函数就是设置随机种子的函数，也就是设置随机函数上一次的状态值。time(0) 将返回一个时间戳，你就可以把他当成和当前时间相关的一个整型数字。 你会发现，上面这段程序中，在第 6 行代码里，我们虽然使用了 rand() 函数，可每次运行都将输出同样的值，这是因为我们没有设置随机种子，每次运行时 rand() 函数所记录的起始值都相同，所以每次运行输出的随机值也都相同。 而第 8 行代码中，由于我们根据程序运行时的当前时间设置了随机种子，每次运行程序，第 8 行都将输出不同的值。事实上，如果你在 srand() 函数里面设置一个固定值，每次运行程序，结果也都将是一样的，这个你可以自行尝试。 至此，我们就准备好了今天任务的全部基础知识了，接下来做道练习题，锻炼一下吧。 ## 一起动手，搞事情 #### 思考题：设计迷你随机函数 >

设计一个循环过程，循环100次，以不太明显的规律输出 1～100 中的每个数字。
要求1：规律尽量不明显。
要求2：只能使用循环和最基本的运算，不允许超前使用数组。

下表是我的程序输出的序列，以供你做参考： ``` 5 15 45 34 1 3 9 27 81 41 22 66 97 89 65 94 80 38 13 39 16 48 43 28 84 50 49 46 37 10 30 90 68 2 6 18 54 61 82 44 31 93 77 29 87 59 76 26 78 32 96 86 56 67100 98 92 74 20 60 79 35 4 12 36 7 21 63 88 62 85 53 58 73 17 51 52 55 64 91 71 11 33 99 95 83 47 40 19 57 70 8 24 72 14 42 25 75 23 69 ``` ## 用有趣的方法计算 π 值 准备完了所有的基础技能后，就让我们来完成开始说的那个任务吧。 我们来思考一下哈，首先我们需要有一个循环，循环每一次，让计算机帮我们做一次实验。每次实验呢，让计算机模拟随机选择点的这个过程，然后我们需要判断一下随机选择的点，是否在圆内部；如果在，我们就记录一次。最后用落在圆里的次数比上总实验次数再乘以4，就得到了 π 的近似值。 这个过程中，你到现在还比较懵的，可能就是随机选点的过程了。那就跟我来看下面代码吧： ``` double x = 1.0 * rand() / RAND_MAX; ``` 上述代码中的 rand() 随机函数，返回值的范围是[0, RAND_MAX]，通过上述表达式计算，我们就得到了一个[0.0, 1.0] 之间的随机值了。 下面就让我们完善程序： ``` #include <stdio.h> #include <stdlib.h> #include <time.h> int main() { int n = 0, m = 0; for (int i = 0; i < 1000000; i++) { double x = 1.0 * rand() / RAND_MAX; double y = 1.0 * rand() / RAND_MAX; if (x * x + y * y <= 1.0) m += 1; n += 1; } printf("%lf\n", 4.0 * m / n); return 0; } ``` 上述代码中，我让计算机重复10万次实验，每次在坐标轴的第一象限中的 1 * 1 的区域中随机选择一个点，变量 m 记录的是落在圆内部的次数，变量 n 记录的是总实验次数。运行这个程序，在我的环境中，输出的是 3.142096，你可以试一下在你的环境中的运行结果，以及加大实验次数以后，对结果的影响。 是不是很难想象，如果没有计算机，我们自己将如何来完成这10万次实验呢？想想都是很痛苦的过程！ ## 课程小结 今天这节课，你了解了C 语言中的随机函数，以及计算机中随机函数的基本原理。最后呢，总结一下今天的重点，就两点： 1. 计算机中都是伪随机函数，也就是说，下一次的随机值，跟本次的随机值是相关的。 1. 使用 srand 函数设置随机种子，也就是设置伪随机过程中的第一个起始点的位置。 理解了上面这两点，也就算是真正理解了计算机中的随机函数的概念了。 从今天开始，记住，计算机就是你的小帮手了，以后的日子里，请动用你的智力，使用它的体力！随着你的思维逻辑越来越严谨，你会爱上这个帮手的，即使它日后可能会因为一些不知名的小 Bug 惹你不开心，相信我，都是暂时的。 好了，今天就到这里了，我是胡光，我们下期见。