今天我带你用数据挖掘对比特币的走势进行预测和分析。 我们之前介绍了数据挖掘算法中的分类、聚类、回归和关联分析算法，那么对于比特币走势的预测，采用哪种方法比较好呢？ 可能有些人会认为采用回归分析会好一些，因为预测的结果是连续的数值类型。实际上，数据挖掘算法还有一种叫时间序列分析的算法，时间序列分析模型建立了观察结果与时间变化的关系，能帮我们预测未来一段时间内的结果变化情况。 那么时间序列分析和回归分析有哪些区别呢？ 首先，在选择模型前，我们需要确定结果与变量之间的关系。回归分析训练得到的是目标变量y与自变量x（一个或多个）的相关性，然后通过新的自变量x来预测目标变量y。而时间序列分析得到的是目标变量y与时间的相关性。 另外，回归分析擅长的是多变量与目标结果之间的分析，即便是单一变量，也往往与时间无关。而时间序列分析建立在时间变化的基础上，它会分析目标变量的趋势、周期、时期和不稳定因素等。这些趋势和周期都是在时间维度的基础上，我们要观察的重要特征。 那么针对今天要进行的预测比特币走势的项目，我们都需要掌握哪些目标呢？

了解时间序列预测的概念，以及常用的模型算法，包括AR、MA、ARMA、ARIMA模型等；

掌握并使用ARMA模型工具，对一个时间序列数据进行建模和预测；

对比特币的历史数据进行时间序列建模，并预测未来6个月的走势。

## 时间序列预测 关于时间序列，你可以把它理解为按照时间顺序组成的数字序列。实际上在中国古代的农业社会中，人们就将一年中不同时间节点和天气的规律总结了下来，形成了二十四节气，也就是从时间序列中观察天气和太阳的规律（只是当时没有时间序列模型和相应工具），从而使得农业得到迅速发展。在现代社会，时间序列在金融、经济、商业领域拥有广泛的应用。 在时间序列预测模型中，有一些经典的模型，包括AR、MA、ARMA、ARIMA。我来给你简单介绍一下。 AR的英文全称叫做Auto Regressive，中文叫自回归模型。这个算法的思想比较简单，它认为过去若干时刻的点通过线性组合，再加上白噪声就可以预测未来某个时刻的点。 在我们日常生活环境中就存在白噪声，在数据挖掘的过程中，你可以把它理解为一个期望为0，方差为常数的纯随机过程。AR模型还存在一个阶数，称为AR（p）模型，也叫作p阶自回归模型。它指的是通过这个时刻点的前p个点，通过线性组合再加上白噪声来预测当前时刻点的值。 MA的英文全称叫做 Moving Average，中文叫做滑动平均模型。它与AR模型大同小异，AR模型是历史时序值的线性组合，MA是通过历史白噪声进行线性组合来影响当前时刻点。AR模型中的历史白噪声是通过影响历史时序值，从而间接影响到当前时刻点的预测值。同样MA模型也存在一个阶数，称为MA(q)模型，也叫作q阶移动平均模型。我们能看到AR和MA模型都存在阶数，在AR模型中，我们用p表示，在MA模型中我们用q表示，这两个模型大同小异，与AR模型不同的是MA模型是历史白噪声的线性组合。 ARMA的英文全称是Auto Regressive Moving Average，中文叫做自回归滑动平均模型，也就是AR模型和MA模型的混合。相比AR模型和MA模型，它有更准确的估计。同样ARMA模型存在p和q两个阶数，称为ARMA(p,q)模型。 ARIMA的英文全称是Auto Regressive Integrated Moving Average模型，中文叫差分自回归滑动平均模型，也叫求合自回归滑动平均模型。相比于ARMA，ARIMA多了一个差分的过程，作用是对不平稳数据进行差分平稳，在差分平稳后再进行建模。ARIMA的原理和ARMA模型一样。相比于ARMA(p,q)的两个阶数，ARIMA是一个三元组的阶数(p,d,q)，称为ARIMA(p,d,q)模型。其中d是差分阶数。 ## ARMA模型工具 上面介绍的AR，MA，ARMA，ARIMA四种模型，你只需要了解基础概念即可，中间涉及到的一些数学公式这里不进行展开。 在实际工作中，我们更多的是使用工具，我在这里主要讲解下如何使用ARMA模型工具。 在使用ARMA工具前，你需要先引用相关工具包： ``` from statsmodels.tsa.arima_model import ARMA ``` 然后通过ARMA(endog,order,exog=None)创建ARMA类，这里有一些主要的参数简单说明下： endog：英文是endogenous variable，代表内生变量，又叫非政策性变量，它是由模型决定的，不被政策左右，可以说是我们想要分析的变量，或者说是我们这次项目中需要用到的变量。 order：代表是p和q的值，也就是ARMA中的阶数。 exog：英文是exogenous variables，代表外生变量。外生变量和内生变量一样是经济模型中的两个重要变量。相对于内生变量而言，外生变量又称作为政策性变量，在经济机制内受外部因素的影响，不是我们模型要研究的变量。 举个例子，如果我们想要创建ARMA(7,0)模型，可以写成：ARMA(data,(7,0))，其中data是我们想要观察的变量，(7,0)代表(p,q)的阶数。 创建好之后，我们可以通过fit函数进行拟合，通过predict(start, end)函数进行预测，其中start为预测的起始时间，end为预测的终止时间。 下面我们使用ARMA模型对一组时间序列做建模，代码如下： ``` # coding:utf-8 # 用ARMA进行时间序列预测 import pandas as pd import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.tsa.arima_model import ARMA from statsmodels.graphics.api import qqplot # 创建数据 data = [5922, 5308, 5546, 5975, 2704, 1767, 4111, 5542, 4726, 5866, 6183, 3199, 1471, 1325, 6618, 6644, 5337, 7064, 2912, 1456, 4705, 4579, 4990, 4331, 4481, 1813, 1258, 4383, 5451, 5169, 5362, 6259, 3743, 2268, 5397, 5821, 6115, 6631, 6474, 4134, 2728, 5753, 7130, 7860, 6991, 7499, 5301, 2808, 6755, 6658, 7644, 6472, 8680, 6366, 5252, 8223, 8181, 10548, 11823, 14640, 9873, 6613, 14415, 13204, 14982, 9690, 10693, 8276, 4519, 7865, 8137, 10022, 7646, 8749, 5246, 4736, 9705, 7501, 9587, 10078, 9732, 6986, 4385, 8451, 9815, 10894, 10287, 9666, 6072, 5418] data=pd.Series(data) data_index = sm.tsa.datetools.dates_from_range('1901','1990') # 绘制数据图 data.index = pd.Index(data_index) data.plot(figsize=(12,8)) plt.show() # 创建ARMA模型# 创建ARMA模型 arma = ARMA(data,(7,0)).fit() print('AIC: %0.4lf' %arma.aic) # 模型预测 predict_y = arma.predict('1990', '2000') # 预测结果绘制 fig, ax = plt.subplots(figsize=(12, 8)) ax = data.ix['1901':].plot(ax=ax) predict_y.plot(ax=ax) plt.show() ``` 运行结果： ``` AIC: 1619.6323 ```
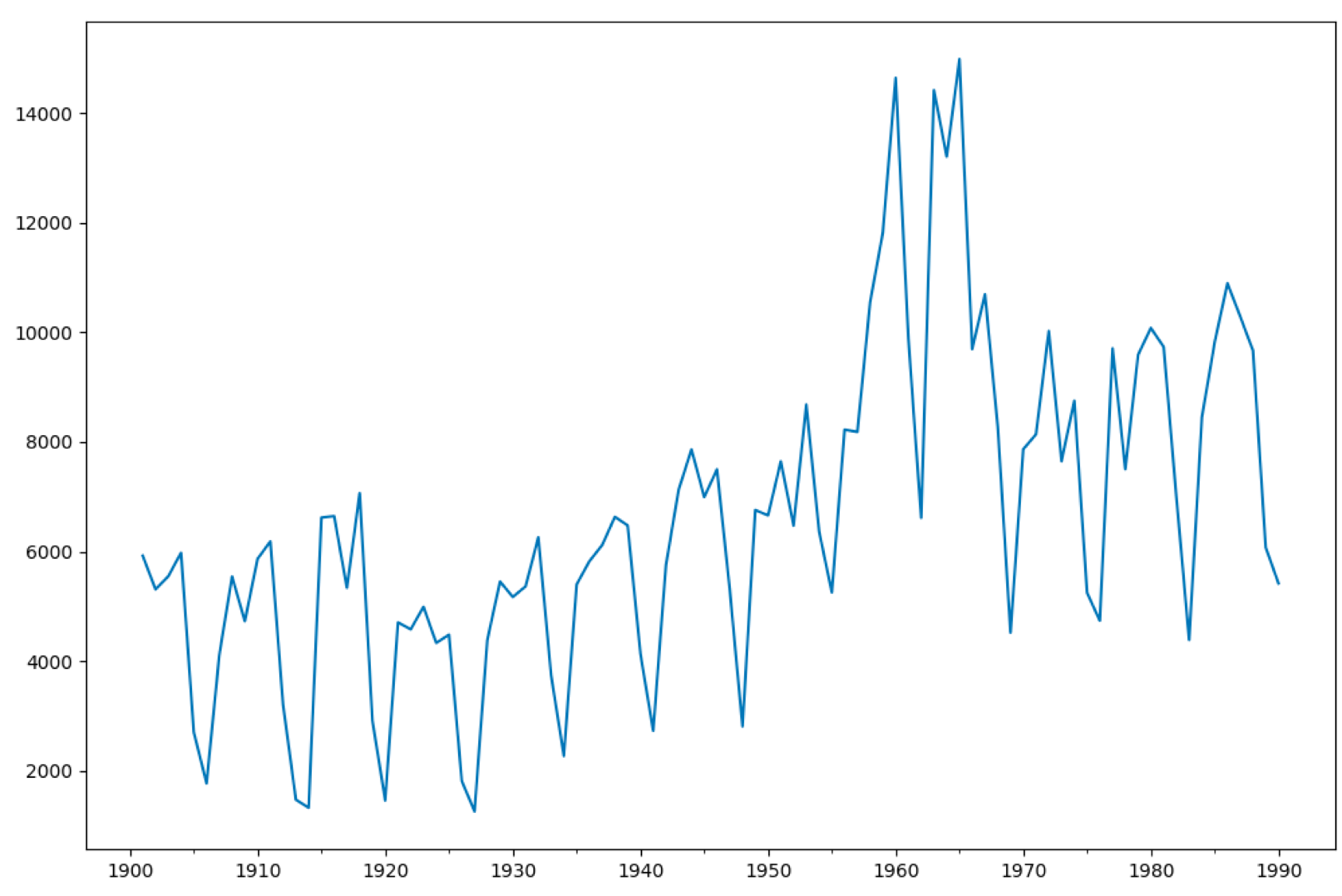
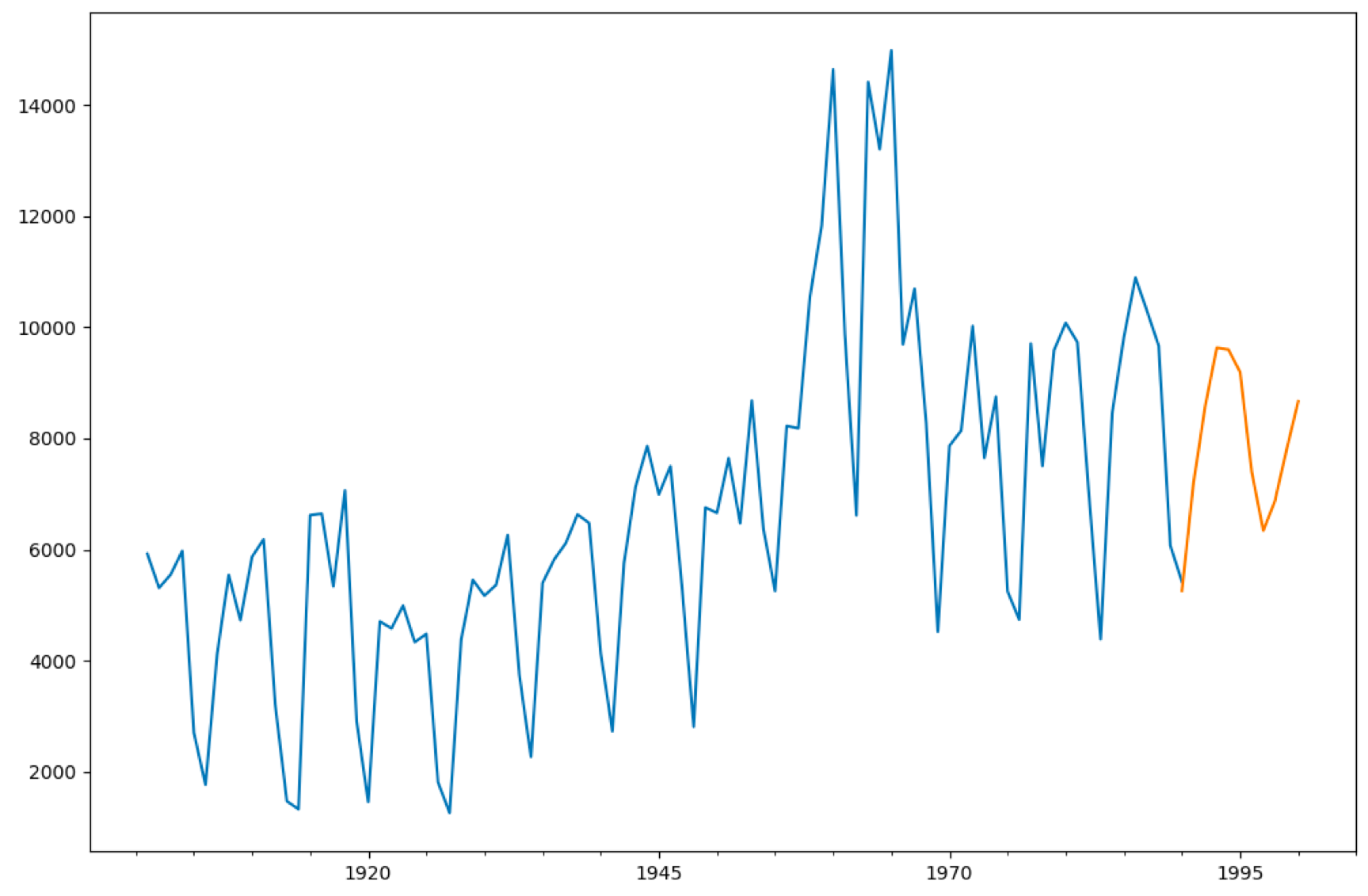
我创建了1901年-1990年之间的时间序列数据data，然后创建ARMA(7,0)模型，并传入时间序列数据data，使用fit函数拟合，然后对1990年-2000年之间的数据进行预测，最后绘制预测结果。 你能看到ARMA工具的使用还是很方便的，只是我们需要p和q的取值。实际项目中，我们可以给p和q指定一个范围，让ARMA都运行一下，然后选择最适合的模型。 你可能会问，怎么判断一个模型是否适合？ 我们需要引入AIC准则，也叫作赤池消息准则，它是衡量统计模型拟合好坏的一个标准，数值越小代表模型拟合得越好。 在这个例子中，你能看到ARMA(7,0)这个模型拟合出来的AIC是1619.6323（并不一定是最优）。 ## 对比特币走势进行预测 我们都知道比特币的走势除了和历史数据以外，还和很多外界因素相关，比如用户的关注度，各国的政策，币圈之间是否打架等等。当然这些外界的因素不是我们这节课需要考虑的对象。 假设我们只考虑比特币以往的历史数据，用ARMA这个时间序列模型预测比特币的走势。 比特币历史数据（从2012-01-01到2018-10-31）可以从GitHub上下载：[https://github.com/cystanford/bitcoin](https://github.com/cystanford/bitcoin)。 你能看到数据一共包括了8个字段，代表的含义如下：
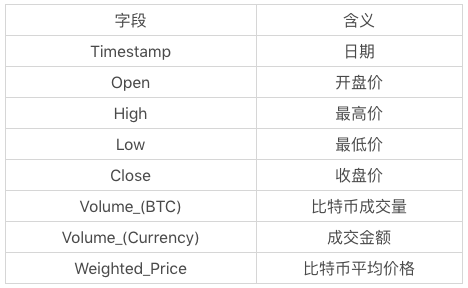
我们的目标是构造ARMA时间序列模型，预测比特币（平均）价格走势。p和q参数具体选择多少呢？我们可以设置一个区间范围，然后选择AIC最低的ARMA模型。 我们梳理下整个项目的流程：
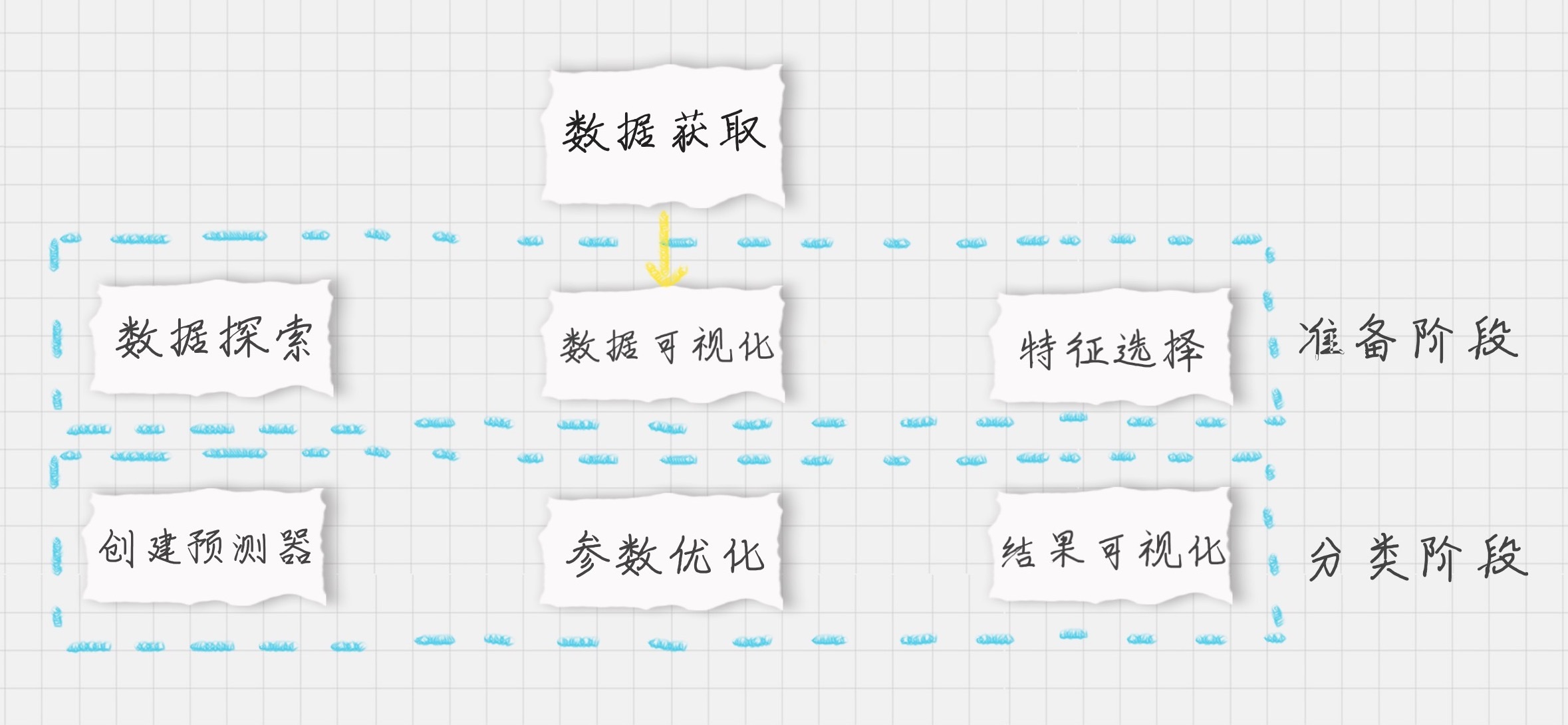
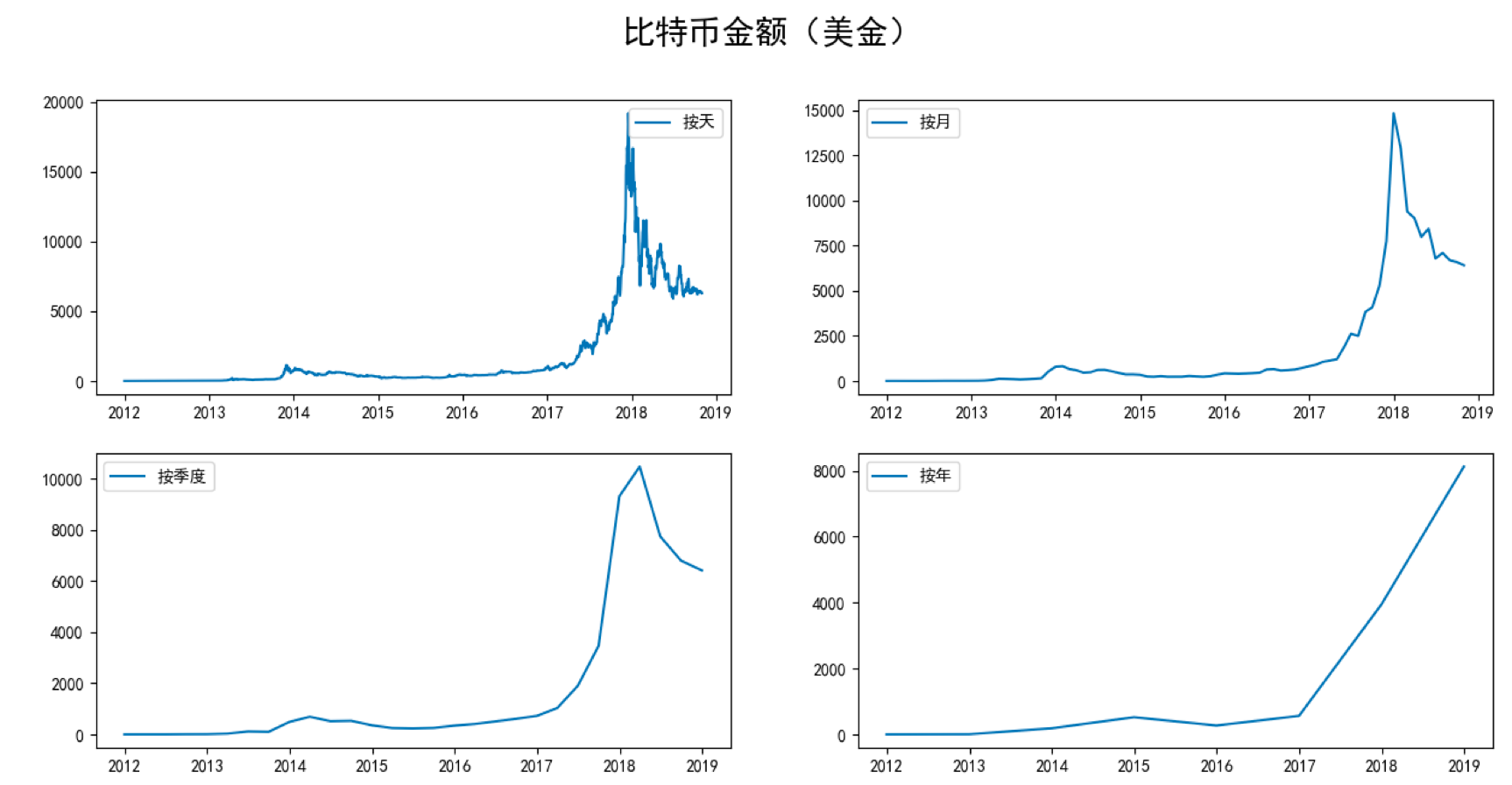
首先我们需要加载数据。 在准备阶段，我们需要先探索数据，采用数据可视化方式查看比特币的历史走势。按照不同的时间尺度（天，月，季度，年）可以将数据压缩，得到不同尺度的数据，然后做可视化呈现。这4个时间尺度上，我们选择月作为预测模型的时间尺度，相应的，我们选择Weighted_Price这个字段的数值作为观察结果，在原始数据中，Weighted_Price对应的是比特币每天的平均价格，当我们以“月”为单位进行压缩的时候，对应的Weighted_Price得到的就是当月的比特币平均价格。压缩代码如下： ``` df_month = df.resample('M').mean() ``` 最后在预测阶段创建ARMA时间序列模型。我们并不知道p和q取什么值时，模型最优，因此我们可以给它们设置一个区间范围，比如都是range(0,3)，然后计算不同模型的AIC数值，选择最小的AIC数值对应的那个ARMA模型。最后用这个最优的ARMA模型预测未来8个月的比特币平均价格走势，并将结果做可视化呈现。 基于这个流程，具体代码如下： ``` # -*- coding: utf-8 -*- # 比特币走势预测，使用时间序列ARMA import numpy as np import pandas as pd import matplotlib.pyplot as plt from statsmodels.tsa.arima_model import ARMA import warnings from itertools import product from datetime import datetime warnings.filterwarnings('ignore') # 数据加载 df = pd.read_csv('./bitcoin_2012-01-01_to_2018-10-31.csv') # 将时间作为df的索引 df.Timestamp = pd.to_datetime(df.Timestamp) df.index = df.Timestamp # 数据探索 print(df.head()) # 按照月，季度，年来统计 df_month = df.resample('M').mean() df_Q = df.resample('Q-DEC').mean() df_year = df.resample('A-DEC').mean() # 按照天，月，季度，年来显示比特币的走势 fig = plt.figure(figsize=[15, 7]) plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签 plt.suptitle('比特币金额（美金）', fontsize=20) plt.subplot(221) plt.plot(df.Weighted_Price, '-', label='按天') plt.legend() plt.subplot(222) plt.plot(df_month.Weighted_Price, '-', label='按月') plt.legend() plt.subplot(223) plt.plot(df_Q.Weighted_Price, '-', label='按季度') plt.legend() plt.subplot(224) plt.plot(df_year.Weighted_Price, '-', label='按年') plt.legend() plt.show() # 设置参数范围 ps = range(0, 3) qs = range(0, 3) parameters = product(ps, qs) parameters_list = list(parameters) # 寻找最优ARMA模型参数，即best_aic最小 results = [] best_aic = float("inf") # 正无穷 for param in parameters_list: try: model = ARMA(df_month.Weighted_Price,order=(param[0], param[1])).fit() except ValueError: print('参数错误:', param) continue aic = model.aic if aic < best_aic: best_model = model best_aic = aic best_param = param results.append([param, model.aic]) # 输出最优模型 result_table = pd.DataFrame(results) result_table.columns = ['parameters', 'aic'] print('最优模型: ', best_model.summary()) # 比特币预测 df_month2 = df_month[['Weighted_Price']] date_list = [datetime(2018, 11, 30), datetime(2018, 12, 31), datetime(2019, 1, 31), datetime(2019, 2, 28), datetime(2019, 3, 31), datetime(2019, 4, 30), datetime(2019, 5, 31), datetime(2019, 6, 30)] future = pd.DataFrame(index=date_list, columns= df_month.columns) df_month2 = pd.concat([df_month2, future]) df_month2['forecast'] = best_model.predict(start=0, end=91) # 比特币预测结果显示 plt.figure(figsize=(20,7)) df_month2.Weighted_Price.plot(label='实际金额') df_month2.forecast.plot(color='r', ls='--', label='预测金额') plt.legend() plt.title('比特币金额（月）') plt.xlabel('时间') plt.ylabel('美金') plt.show() ``` 运行结果： ``` Timestamp ... Weighted_Price Timestamp ... 2011-12-31 2011-12-31 ... 4.471603 2012-01-01 2012-01-01 ... 4.806667 2012-01-02 2012-01-02 ... 5.000000 2012-01-03 2012-01-03 ... 5.252500 2012-01-04 2012-01-04 ... 5.208159 [5 rows x 8 columns] ```
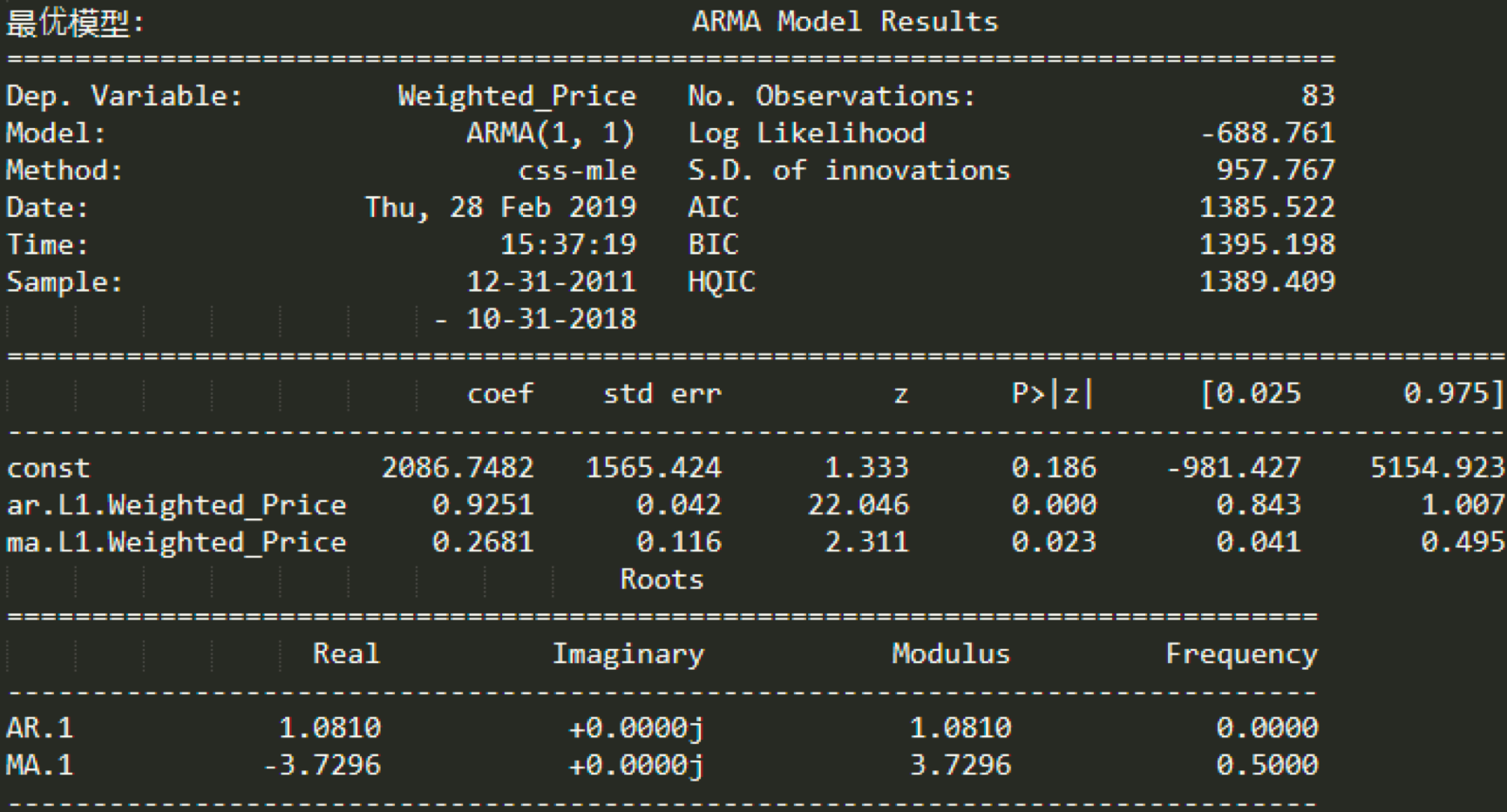
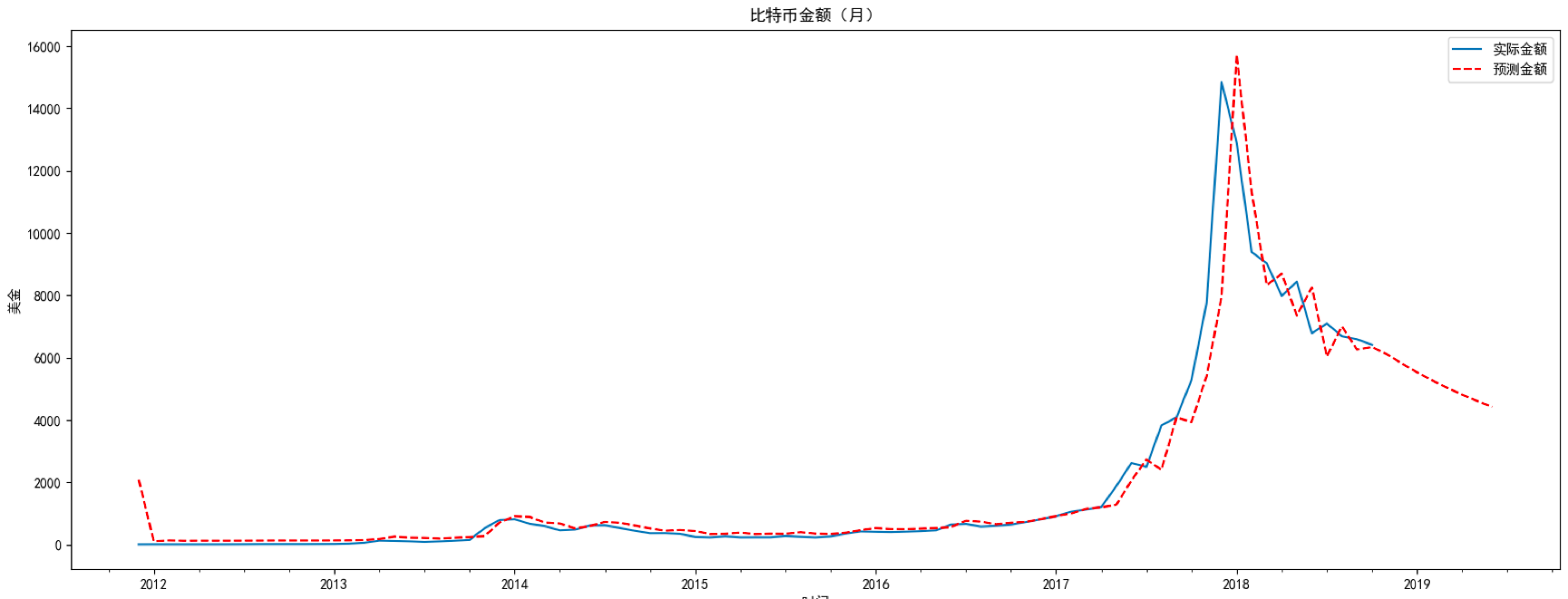
我们通过product函数创建了(p,q)在range(0,3)范围内的所有可能组合，并对每个ARMA(p,q)模型进行了AIC数值计算，保存了AIC数值最小的模型参数。然后用这个模型对比特币的未来8个月进行了预测。 从结果中你能看到，在2018年10月之后8个月的时间里，比特币会触底到4000美金左右，实际上比特币在这个阶段确实降低到了4000元美金甚至更低。在时间尺度的选择上，我们选择了月，这样就对数据进行了降维，也节约了ARMA的模型训练时间。你能看到比特币金额（美金）这张图中，按月划分的比特币走势和按天划分的比特币走势差别不大，在减少了局部的波动的同时也能体现出比特币的趋势，这样就节约了ARMA的模型训练时间。 ## 总结 今天我给你讲了一个比特币趋势预测的实战项目。通过这个项目你应该能体会到，当我们对一个数值进行预测的时候，如果考虑的是多个变量和结果之间的关系，可以采用回归分析，如果考虑单个时间维度与结果的关系，可以使用时间序列分析。 根据比特币的历史数据，我们使用ARMA模型对比特币未来8个月的走势进行了预测，并对结果进行了可视化显示。你能看到ARMA工具还是很好用的，虽然比特币的走势受很多外在因素影响，比如政策环境。不过当我们掌握了这些历史数据，也不妨用时间序列模型来分析预测一下。
最后依然是思考题环节，今天我们讲了AR、MA、ARMA和ARIMA，你能简单说说它们之间的区别么？ 另外我在[GitHub](https://github.com/cystanford/bitcoin)中上传了沪市指数的历史数据（对应的shanghai_1990-12-19_to_2019-2-28.csv），请你编写代码使用ARMA模型对沪市指数未来10个月（截止到2019年12月31日）的变化进行预测（将数据转化为按月统计即可）。 欢迎你在评论区与我分享你的答案，也欢迎点击“请朋友读”，把这篇文章分享给你的朋友或者同事。