你好,我是黄申。
之前我使用Boston Housing的数据,阐述了如何使用多元线性回归。可是,计算机系统究竟是如何根据观测到的数据,来拟合线性回归模型呢?这两节,我就从最简单的线性方程组出发,来说说如何求解线性回归的问题。
在第29讲中,我讲过机器学习中两类很重要的方法:回归分析以及线性回归。回归分析属于监督式学习算法,主要研究一个或多个随机变量$y_1$,$y_2$,…,$y_i$与另一些变量$x_{1}$,$x_{2}$,…,$x_{k}$之间的关系。其中,我们将$y_{1},y_{2}、…,y_{i}$称为因变量,$x_1,x_2,…,x_k$称为自变量。按照不同的维度,我们可以把回归分为三种。
按照自变量数量,当自变量$x$的个数大于1时就是多元回归。
按照因变量数量,当因变量$y$个数大于1时就是多重回归。
按照模型种类,如果因变量和自变量为线性关系时,就是线性回归模型;如果因变量和自变量为非线性关系时时,就是非线性回归分析模型。
## 高斯消元法
对于回归分析来说,最简单的情形是只有一个自变量和一个因变量,且它们大体上是有线性关系的,这就是一元线性回归。对应的模型很简单,就是$Y=a+bX+ε$。这里的$X$是自变量,$Y$是因变量,$a$是截距,b是自变量的系数。前面这些你估计都很熟悉,最后还有个$ε$,这表示随机误差,只不过我们通常假定随机误差的均值为$0$。进一步来说,如果我们暂时不考虑a和ε,把它扩展为多元的形式,那么就可以得到类似下面这种形式的方程:
$b_1·x_1+b_2·x_2+...+b_{n-1}·x_{n-1} +b_n·x_n=y$
假设我们有多个这样的方程,就能构成线性方程组,我这里列出一个例子。
$2x_1+x_2+x_3=0$
$4x_1+2x_2+x_3=56$
$2x_1-x_2+4x_3=4$
对于上面这个方程组,如果存在至少一组$x_1、x_2$和$x_3$使得三个方程都成立,那么就叫方程有解;如果没有,那么我们就说方程无解。如果方程有解,那么解可能是唯一,也可能是多个。我们通常关心的是,方程组是不是有解,以及$x_1$一直到$x_n$分别是多少。
为了实现这个目的,人们想了很多方法来求解方程组,这些方法看起来多种多样,其实主要就是两大类,直接法和迭代法。
直接法就是通过有限次的算术运算,计算精确解。而迭代法,我们在第3讲就提到过,它是一种不断用变量的旧值递推新值的过程。我们可以用迭代法不断地逼近方程的精确解。
这里,我就从上面这个方程组的例子出发,阐述最常见的高斯消元法,以及如何使用矩阵操作来实现它。
高斯消元法主要分为两步,**消元**(Forward Elimination)和**回代**(Back Substitution)。所谓消元,就是要减少某些方程中元的数量。如果某个方程中的元只剩一个了$x_m$了,那么这个自变量$x_m$的解就能知道了。所谓的回代,就是把已知的解$x_m$代入到方程式中,求出其他未知的解。
我们先从消元开始,来看这个方程组。
$2x_1+x_2+x_3=0$
$4x_1+2x_2+x_3=56$
$2x_1-x_2+4x_3=4$
首先保持第一个方程不变,然后消除第二个和第三个方程中的$x_1$。对于第二个方程,方法是让第二个方程式减去第一个方程式的两倍,方程的左侧为:
$(4x_1+2x_2+x_3)-2(2x_1+x_2+x_3)=-x_3$
方程的右侧变为:
$56-2·0=56$
所以第二个方程变为:
$-x_3=56$
这样三个方程式就变为:
$2x_1+x_2+x_3=0$
$-x_3=56$
$2x_1-x_2+4x_3=4$
对于第三个方程同样如此,我们需要去掉其中的$x_1$。方法是让第三个方程减去第一个方程,之后三个方程式变为:
$2x_1+x_2+x_3=0$
$-x_3=56$
$-2x_2+3x_3=4$
至此,我们使用第一个方程式作为参照,消除了第二个和第三个方程式中的$x_1$,我们称这里的第一个方程式为“主元行”。
接下来,我们要把第二个方程式作为“主元行”,来消除第三个方程中的$x_2$。你应该能发现,第二个方程中的$x_2$已经没有了,失去了参照,这个时候我们需要把第二个方程和第三个方程互换,变为:
$2x_1+x_2+x_3=0$
$-2x_2+3x_3=4$
$-x_3=56$
到了这个时候,由于第三个方程以及没有$x_2$了,所以无需再消元。如果还有$x_2$,那么就需要参照第二个方程式来消除第三个方程中的$x_2$。
观察一下现在的方程组,第一个方程有3个自变量,第二个方程有2个自变量,第三个方程只有1个自变量。这个时候,我们就可以从第三个方程开始,开始回代的过程了。通过第三个方程,显然我们可以得到$x_3=-56$,然后把这个值代入第二个方程,就可以得到$x_2 = -86$。最后把$x_2$和$x_3$的值代入第一个方程式,我们可以得到$x_1=71$。
## 使用矩阵实现高斯消元法
如果方程和元的数量很小,那么高斯消元法并不难理解。可是如果方程和元的数量很多,整个过程就变得比较繁琐了。实际上,我们可以把高斯消元法转为矩阵的操作,便于自己的理解和记忆。
为了进行矩阵操作,首先我们要把方程中的系数$b_i$转成矩阵,我们把这个矩阵记作$B$。对于上面的方程组示例,系数矩阵为:
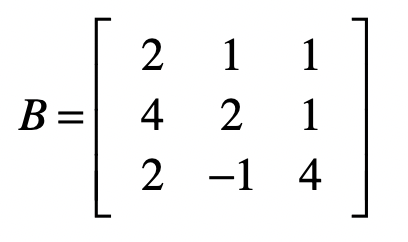 那么,最终我们通过消元,把系数矩阵B变为:
那么,最终我们通过消元,把系数矩阵B变为:
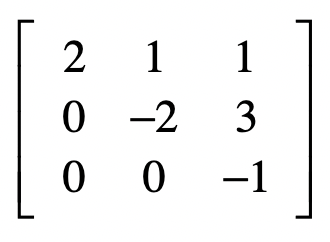 从此可以看出,消元的过程就是把原始的系数矩阵变为上三角矩阵。这里的上三角矩阵表示,矩阵中只有主对角线以及主对角线以上的三角部分里有数字。我们用$U$表示上三角矩阵。
而回代呢,我们最终得到的结果是:
$x_1=71$
从此可以看出,消元的过程就是把原始的系数矩阵变为上三角矩阵。这里的上三角矩阵表示,矩阵中只有主对角线以及主对角线以上的三角部分里有数字。我们用$U$表示上三角矩阵。
而回代呢,我们最终得到的结果是:
$x_1=71$
$x_2=-86$
$x_3=-56$
我们可以把这几个结果看作:
$1·x_1+0·x_2+0·x_3=71$
$0·x_1+1·x_2+0·x_3=-86$
$0·x_1+0·x_2+1·x_3=-56$
再把系数写成矩阵的形式,就是:
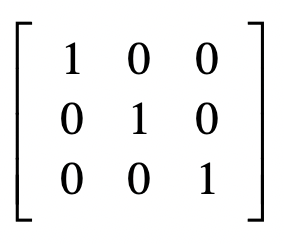 发现没?这其实就是单位矩阵。所以说,回代的过程是把上三角矩阵变为单位矩阵的过程。
为了便于后面的回代计算,我们也可以把方程式等号右边的值加入到系数矩阵,我们称这个新的矩阵为**增广矩阵**,我把这个矩阵记为$A$。
好,现在让我们来观察一下这个增广矩阵$A$。
发现没?这其实就是单位矩阵。所以说,回代的过程是把上三角矩阵变为单位矩阵的过程。
为了便于后面的回代计算,我们也可以把方程式等号右边的值加入到系数矩阵,我们称这个新的矩阵为**增广矩阵**,我把这个矩阵记为$A$。
好,现在让我们来观察一下这个增广矩阵$A$。
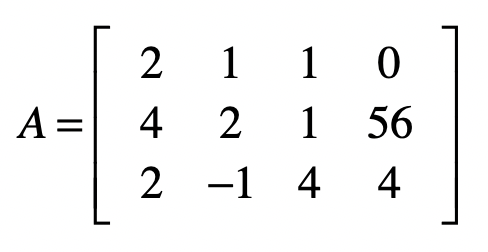 对于这个矩阵,我们的最终目标是,把除了最后一列之外的部分,变成单位矩阵,而此时最后一列中的每个值,就是每个自变量所对应的解了。
之前我已经讲过矩阵相乘在向量空间模型、PageRank算法和协同过滤推荐中的应用。这里,我们同样可以使用这种操作来进行消元。为了方便你理解,我们可以遵循之前消元的步骤一步步来看。
还记得这个方程组消元的第一步吗?对,首先保持第一个方程不变,然后消除第二个和第三个方程中的$x_1$。这就意味着要把$A_{2,1}$和$A_{3,1}$变为$0$。
对于第一个方程式,如果要保持它不变,我们可以让向量$[1, 0, 0]$左乘$A$。对于第二个方程,具体操作是让第二个方程式减去第一个方程式的两倍,达到消除$x_1$的目的。我们可以让向量$[-2, 1, 0]$左乘$A$。对于第三个方程式,具体操作是让第三个方程式减去第一个方程式,达到消除$x_1$的目的。我们可以让向量$[-1, 0, 1]$左乘$A$。我们使用这三个行向量组成一个矩阵$E1$。
对于这个矩阵,我们的最终目标是,把除了最后一列之外的部分,变成单位矩阵,而此时最后一列中的每个值,就是每个自变量所对应的解了。
之前我已经讲过矩阵相乘在向量空间模型、PageRank算法和协同过滤推荐中的应用。这里,我们同样可以使用这种操作来进行消元。为了方便你理解,我们可以遵循之前消元的步骤一步步来看。
还记得这个方程组消元的第一步吗?对,首先保持第一个方程不变,然后消除第二个和第三个方程中的$x_1$。这就意味着要把$A_{2,1}$和$A_{3,1}$变为$0$。
对于第一个方程式,如果要保持它不变,我们可以让向量$[1, 0, 0]$左乘$A$。对于第二个方程,具体操作是让第二个方程式减去第一个方程式的两倍,达到消除$x_1$的目的。我们可以让向量$[-2, 1, 0]$左乘$A$。对于第三个方程式,具体操作是让第三个方程式减去第一个方程式,达到消除$x_1$的目的。我们可以让向量$[-1, 0, 1]$左乘$A$。我们使用这三个行向量组成一个矩阵$E1$。
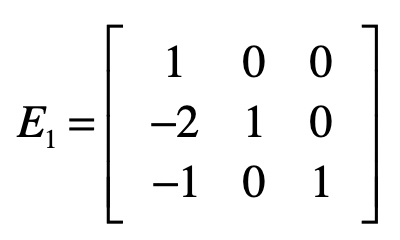 因此,我们可是用下面这个矩阵$E1$和$A$的点乘,来实现消除第二个和第三个方程式中$x_1$的目的。
因此,我们可是用下面这个矩阵$E1$和$A$的点乘,来实现消除第二个和第三个方程式中$x_1$的目的。
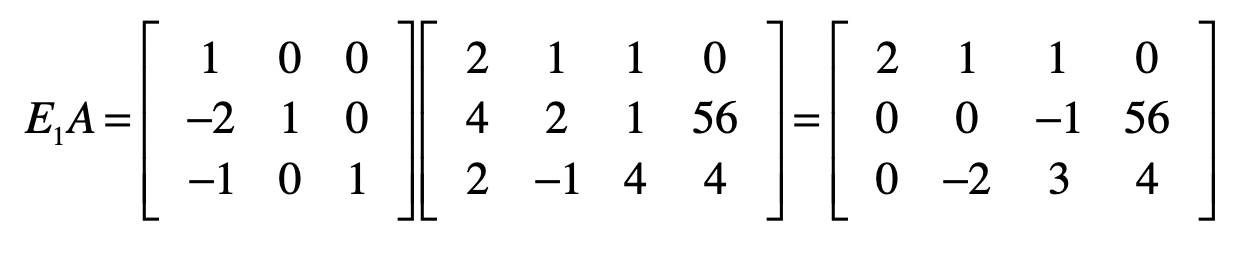 你会发现,由于使用了增广矩阵,矩阵中最右边的一列,也就是方程等号右边的数值也会随之发生改变。
下一步是消除第三个方程中的$x_2$。依照之前的经验,我们要把第二个方程式作为“主元行”,来消除第三个方程中的$x_2$。可是第二个方程中的$x_2$已经没有了,失去了参照,这个时候我们需要把第二个方程和第三个方程互换。这种互换的操作如何使用矩阵来实现呢?其实不难,例如使用下面这个矩阵$E2$左乘增广矩阵$A$。
你会发现,由于使用了增广矩阵,矩阵中最右边的一列,也就是方程等号右边的数值也会随之发生改变。
下一步是消除第三个方程中的$x_2$。依照之前的经验,我们要把第二个方程式作为“主元行”,来消除第三个方程中的$x_2$。可是第二个方程中的$x_2$已经没有了,失去了参照,这个时候我们需要把第二个方程和第三个方程互换。这种互换的操作如何使用矩阵来实现呢?其实不难,例如使用下面这个矩阵$E2$左乘增广矩阵$A$。
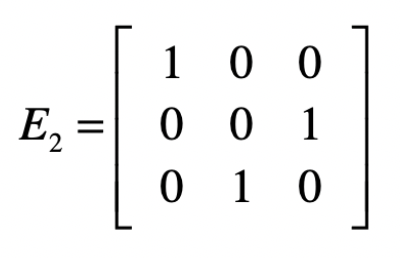 上面这个矩阵第一行$[1 0 0]$的意思就是我们只取第一行的方程,而第二行$[0 0 1]$的意思是只取第三个方程,而第三行$[0 1 0]$表示只取第二个方程。
我们先让$E1$左乘$A$,然后再让$E2$左乘$E1A$的结果,就能得到消元后的系数矩阵。
上面这个矩阵第一行$[1 0 0]$的意思就是我们只取第一行的方程,而第二行$[0 0 1]$的意思是只取第三个方程,而第三行$[0 1 0]$表示只取第二个方程。
我们先让$E1$左乘$A$,然后再让$E2$左乘$E1A$的结果,就能得到消元后的系数矩阵。
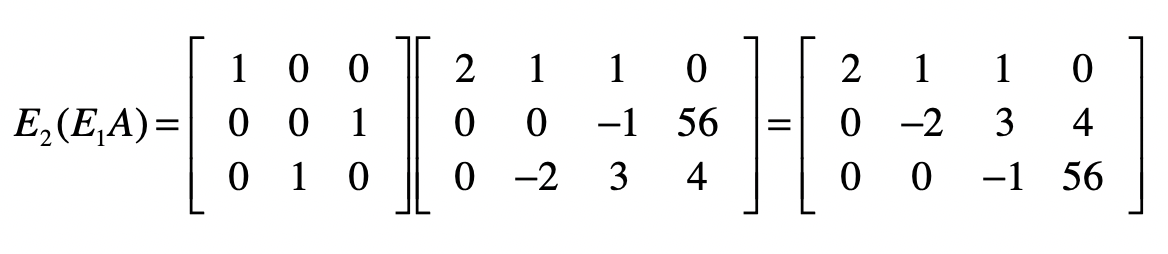 我们把$E1$点乘$E2$的结果记作$E3$,并把$E3$称为消元矩阵。
我们把$E1$点乘$E2$的结果记作$E3$,并把$E3$称为消元矩阵。
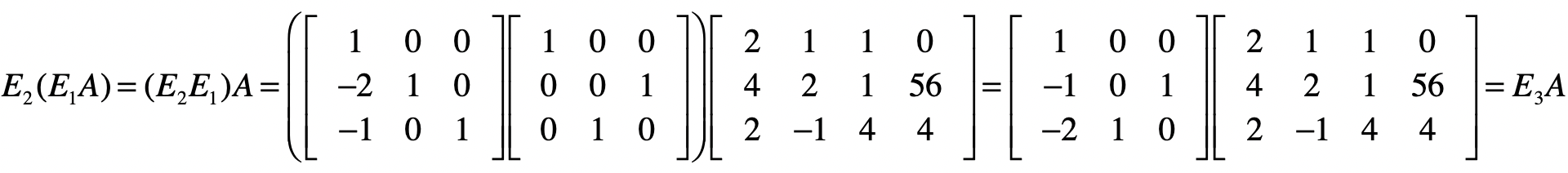
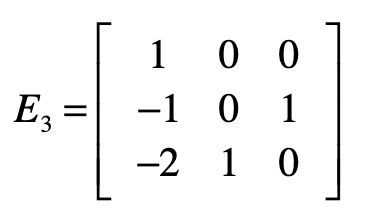 对于目前的结果矩阵来说,除了最后一列,它已经变成了一个上三角矩阵,也就是说消元步骤完成。接下来,我们要使得最后一列之外的部分变成一个单位矩阵,就能得到最终的方程组解。和消元不同的是,我们将从最后一行开始。对于最后一个方程,我们只需要把所有系数取反就行了,所以会使用下面这个矩阵$S1$实现。
对于目前的结果矩阵来说,除了最后一列,它已经变成了一个上三角矩阵,也就是说消元步骤完成。接下来,我们要使得最后一列之外的部分变成一个单位矩阵,就能得到最终的方程组解。和消元不同的是,我们将从最后一行开始。对于最后一个方程,我们只需要把所有系数取反就行了,所以会使用下面这个矩阵$S1$实现。
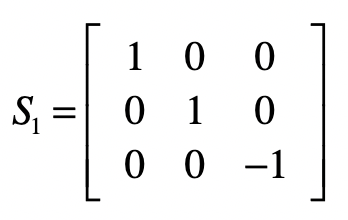
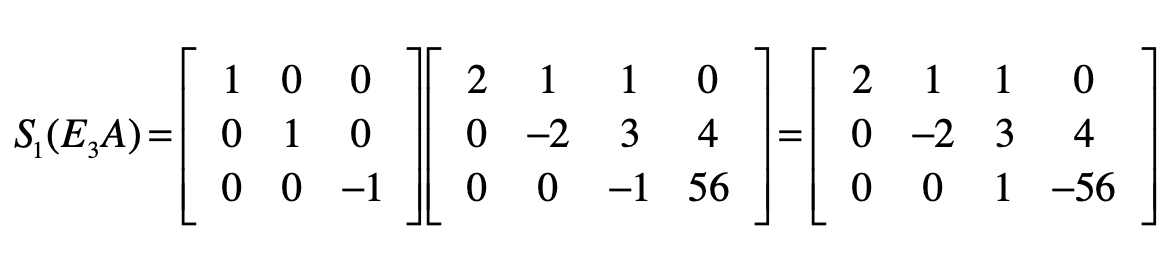 接下来要去掉第二个方程中的$x_3$,我们要把第二个方程减去3倍的第三个方程,然后除以-2。首先是减去3倍的第三个方程。
接下来要去掉第二个方程中的$x_3$,我们要把第二个方程减去3倍的第三个方程,然后除以-2。首先是减去3倍的第三个方程。
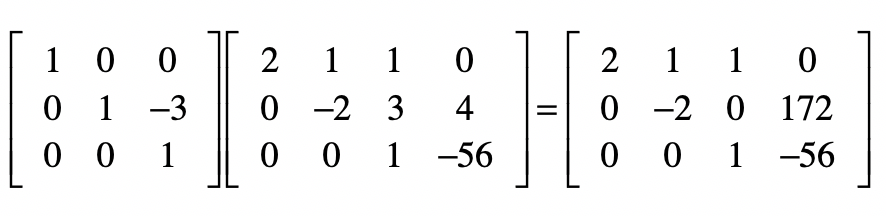 然后把第二个方程除以-2。
然后把第二个方程除以-2。
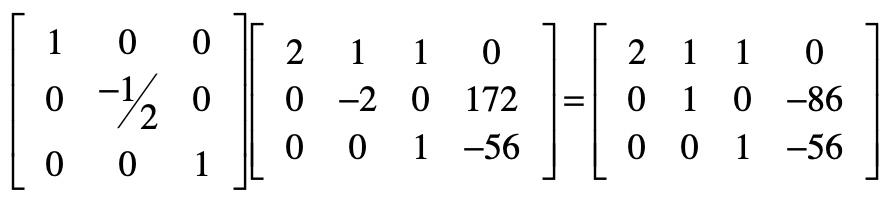 最后,对于第一个方程,我们要把第一个方程减去第二个和第三个方程,最后除以2,我把这几步合并了,并列在下方。
最后,对于第一个方程,我们要把第一个方程减去第二个和第三个方程,最后除以2,我把这几步合并了,并列在下方。
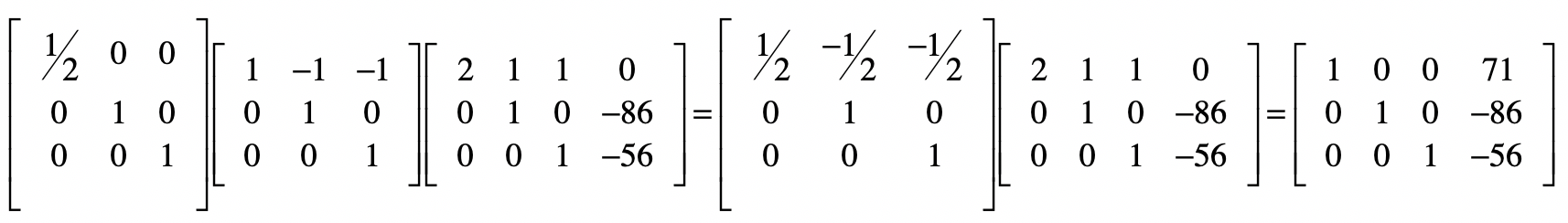 最终,结果矩阵的最后一列就是方程组的解。我们把回代部分的矩阵,都点乘起来。
最终,结果矩阵的最后一列就是方程组的解。我们把回代部分的矩阵,都点乘起来。
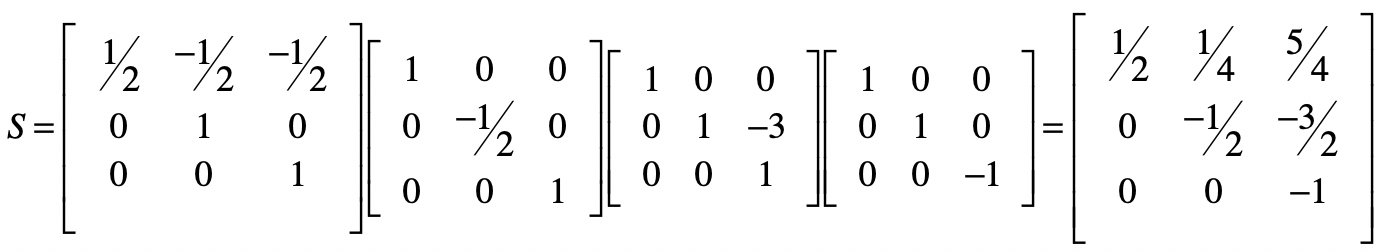 而消元矩阵$E3$为:
而消元矩阵$E3$为:
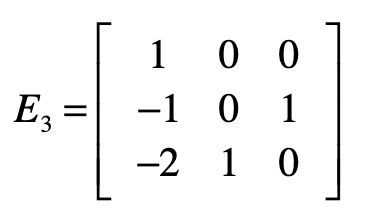 我们可以让矩阵$S$左乘矩阵$E3$,就会得到下面的结果。
我们可以让矩阵$S$左乘矩阵$E3$,就会得到下面的结果。
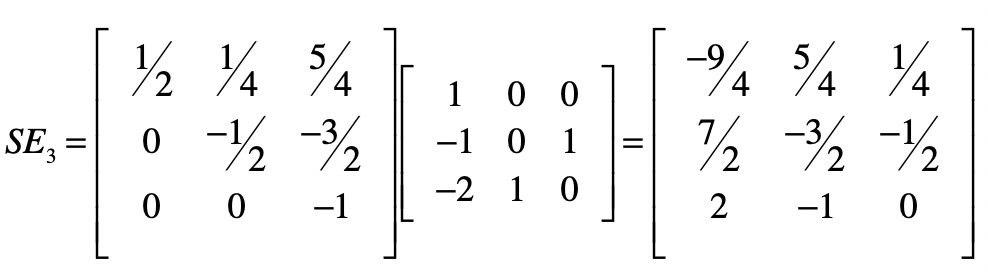 我们把这个矩阵记作$SE$,把乘以最初的系数矩阵$B$,就得到了一个单位矩阵。根据逆矩阵的定义,$SE$就是$B$的逆矩阵。换个角度来思考,使用消元法进行线性方程组求解的过程,就是在找系数矩阵的逆矩阵的过程。
## 总结
今天我们一起探讨了求解线性方程组最常见的方法之一,高斯消元法。这个方法主要包含了消元和回代两个步骤。这些步骤都可以使用矩阵的操作来进行。从矩阵的角度来说,消元就是把系数矩阵变为上三角矩阵,而回代是把这个上三角矩阵变为单位矩阵。我们可以直接把用于消元和回代的矩阵,用于由系数和因变量值组成的增广矩阵,并获得最终的方程解。
线性方程组的概念,也是线性回归分析的基础。在线性回归时,我们也能获得由很多观测数据值所组成的方程组。但是,在进行线性回归分析时,方程组的处理方式和普通的方程组求解有一些不同。其中有两个最主要的区别。
第一个区别是,在线性回归分析中,样本数据会告诉我们自变量和因变量的值,要求的是系数。而在线性方程组中,我们已知系数和因变量的值,要求的是自变量的值。
第二个区别是,在线性回归分析中,方程的数量要远远大于自变量的数量,而且我们不要求每个方程式都是完全成立。这里,不要求完全成立的意思是,拟合出来的因变量值可以和样本数据给定的因变量值存在差异,也就允许模型拟合存在误差。模型拟合的概念我在上一模块的总结篇中重点讲解了,所以你应该能理解,模型的拟合不可能100%完美,这和我们求解线性方程组精确解的概念是不同的。
正是因为这两点差异,我们无法直接使用消元法来求解线性回归。下一节,我会来详细解释,如何使用最小二乘法来解决线性回归的问题。
## 思考题
请分别写出下面这个方程组的消元矩阵和回代矩阵,并求出最终的解。
$x_1-2x_2+x_3-4x_4=4$
我们把这个矩阵记作$SE$,把乘以最初的系数矩阵$B$,就得到了一个单位矩阵。根据逆矩阵的定义,$SE$就是$B$的逆矩阵。换个角度来思考,使用消元法进行线性方程组求解的过程,就是在找系数矩阵的逆矩阵的过程。
## 总结
今天我们一起探讨了求解线性方程组最常见的方法之一,高斯消元法。这个方法主要包含了消元和回代两个步骤。这些步骤都可以使用矩阵的操作来进行。从矩阵的角度来说,消元就是把系数矩阵变为上三角矩阵,而回代是把这个上三角矩阵变为单位矩阵。我们可以直接把用于消元和回代的矩阵,用于由系数和因变量值组成的增广矩阵,并获得最终的方程解。
线性方程组的概念,也是线性回归分析的基础。在线性回归时,我们也能获得由很多观测数据值所组成的方程组。但是,在进行线性回归分析时,方程组的处理方式和普通的方程组求解有一些不同。其中有两个最主要的区别。
第一个区别是,在线性回归分析中,样本数据会告诉我们自变量和因变量的值,要求的是系数。而在线性方程组中,我们已知系数和因变量的值,要求的是自变量的值。
第二个区别是,在线性回归分析中,方程的数量要远远大于自变量的数量,而且我们不要求每个方程式都是完全成立。这里,不要求完全成立的意思是,拟合出来的因变量值可以和样本数据给定的因变量值存在差异,也就允许模型拟合存在误差。模型拟合的概念我在上一模块的总结篇中重点讲解了,所以你应该能理解,模型的拟合不可能100%完美,这和我们求解线性方程组精确解的概念是不同的。
正是因为这两点差异,我们无法直接使用消元法来求解线性回归。下一节,我会来详细解释,如何使用最小二乘法来解决线性回归的问题。
## 思考题
请分别写出下面这个方程组的消元矩阵和回代矩阵,并求出最终的解。
$x_1-2x_2+x_3-4x_4=4$
$x_2-x_3+x_4=-3$
$x_1+3x_2+x_4=1$
$-7x_2+3x_3+x_4=-3$
欢迎留言和我分享,也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
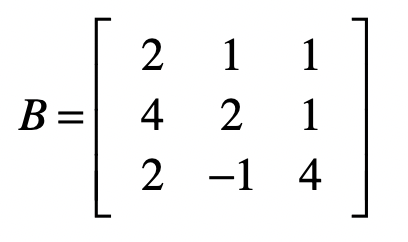 那么,最终我们通过消元,把系数矩阵B变为:
那么,最终我们通过消元,把系数矩阵B变为:
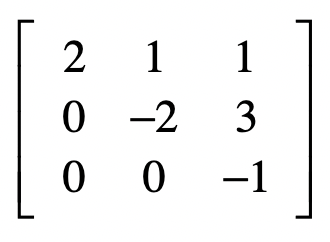 从此可以看出,消元的过程就是把原始的系数矩阵变为上三角矩阵。这里的上三角矩阵表示,矩阵中只有主对角线以及主对角线以上的三角部分里有数字。我们用$U$表示上三角矩阵。
而回代呢,我们最终得到的结果是:
$x_1=71$
从此可以看出,消元的过程就是把原始的系数矩阵变为上三角矩阵。这里的上三角矩阵表示,矩阵中只有主对角线以及主对角线以上的三角部分里有数字。我们用$U$表示上三角矩阵。
而回代呢,我们最终得到的结果是:
$x_1=71$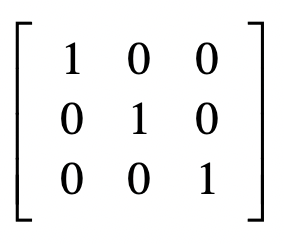 发现没?这其实就是单位矩阵。所以说,回代的过程是把上三角矩阵变为单位矩阵的过程。
为了便于后面的回代计算,我们也可以把方程式等号右边的值加入到系数矩阵,我们称这个新的矩阵为**增广矩阵**,我把这个矩阵记为$A$。
好,现在让我们来观察一下这个增广矩阵$A$。
发现没?这其实就是单位矩阵。所以说,回代的过程是把上三角矩阵变为单位矩阵的过程。
为了便于后面的回代计算,我们也可以把方程式等号右边的值加入到系数矩阵,我们称这个新的矩阵为**增广矩阵**,我把这个矩阵记为$A$。
好,现在让我们来观察一下这个增广矩阵$A$。
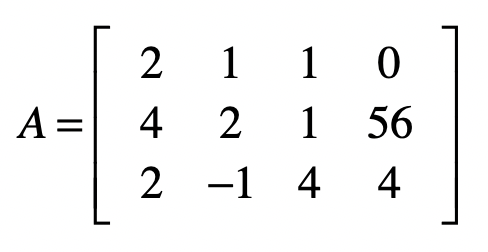 对于这个矩阵,我们的最终目标是,把除了最后一列之外的部分,变成单位矩阵,而此时最后一列中的每个值,就是每个自变量所对应的解了。
之前我已经讲过矩阵相乘在向量空间模型、PageRank算法和协同过滤推荐中的应用。这里,我们同样可以使用这种操作来进行消元。为了方便你理解,我们可以遵循之前消元的步骤一步步来看。
还记得这个方程组消元的第一步吗?对,首先保持第一个方程不变,然后消除第二个和第三个方程中的$x_1$。这就意味着要把$A_{2,1}$和$A_{3,1}$变为$0$。
对于第一个方程式,如果要保持它不变,我们可以让向量$[1, 0, 0]$左乘$A$。对于第二个方程,具体操作是让第二个方程式减去第一个方程式的两倍,达到消除$x_1$的目的。我们可以让向量$[-2, 1, 0]$左乘$A$。对于第三个方程式,具体操作是让第三个方程式减去第一个方程式,达到消除$x_1$的目的。我们可以让向量$[-1, 0, 1]$左乘$A$。我们使用这三个行向量组成一个矩阵$E1$。
对于这个矩阵,我们的最终目标是,把除了最后一列之外的部分,变成单位矩阵,而此时最后一列中的每个值,就是每个自变量所对应的解了。
之前我已经讲过矩阵相乘在向量空间模型、PageRank算法和协同过滤推荐中的应用。这里,我们同样可以使用这种操作来进行消元。为了方便你理解,我们可以遵循之前消元的步骤一步步来看。
还记得这个方程组消元的第一步吗?对,首先保持第一个方程不变,然后消除第二个和第三个方程中的$x_1$。这就意味着要把$A_{2,1}$和$A_{3,1}$变为$0$。
对于第一个方程式,如果要保持它不变,我们可以让向量$[1, 0, 0]$左乘$A$。对于第二个方程,具体操作是让第二个方程式减去第一个方程式的两倍,达到消除$x_1$的目的。我们可以让向量$[-2, 1, 0]$左乘$A$。对于第三个方程式,具体操作是让第三个方程式减去第一个方程式,达到消除$x_1$的目的。我们可以让向量$[-1, 0, 1]$左乘$A$。我们使用这三个行向量组成一个矩阵$E1$。
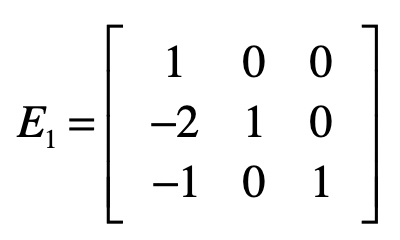 因此,我们可是用下面这个矩阵$E1$和$A$的点乘,来实现消除第二个和第三个方程式中$x_1$的目的。
因此,我们可是用下面这个矩阵$E1$和$A$的点乘,来实现消除第二个和第三个方程式中$x_1$的目的。
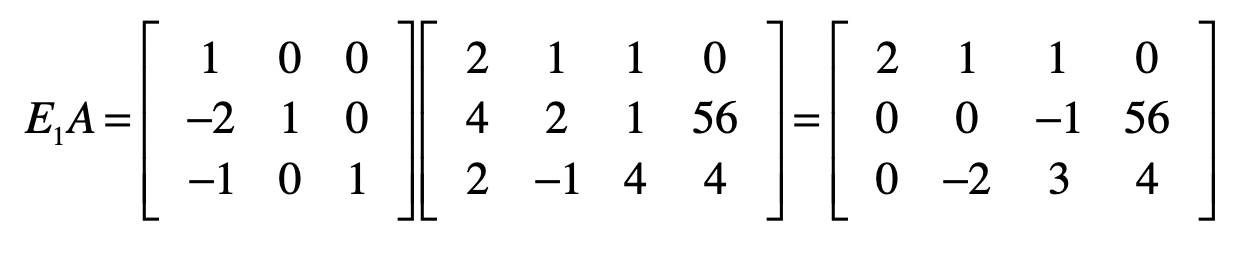 你会发现,由于使用了增广矩阵,矩阵中最右边的一列,也就是方程等号右边的数值也会随之发生改变。
下一步是消除第三个方程中的$x_2$。依照之前的经验,我们要把第二个方程式作为“主元行”,来消除第三个方程中的$x_2$。可是第二个方程中的$x_2$已经没有了,失去了参照,这个时候我们需要把第二个方程和第三个方程互换。这种互换的操作如何使用矩阵来实现呢?其实不难,例如使用下面这个矩阵$E2$左乘增广矩阵$A$。
你会发现,由于使用了增广矩阵,矩阵中最右边的一列,也就是方程等号右边的数值也会随之发生改变。
下一步是消除第三个方程中的$x_2$。依照之前的经验,我们要把第二个方程式作为“主元行”,来消除第三个方程中的$x_2$。可是第二个方程中的$x_2$已经没有了,失去了参照,这个时候我们需要把第二个方程和第三个方程互换。这种互换的操作如何使用矩阵来实现呢?其实不难,例如使用下面这个矩阵$E2$左乘增广矩阵$A$。
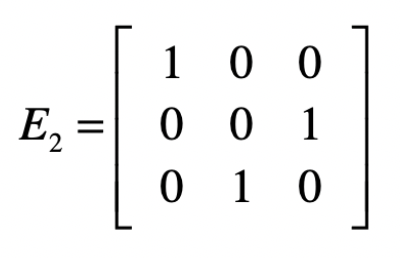 上面这个矩阵第一行$[1 0 0]$的意思就是我们只取第一行的方程,而第二行$[0 0 1]$的意思是只取第三个方程,而第三行$[0 1 0]$表示只取第二个方程。
我们先让$E1$左乘$A$,然后再让$E2$左乘$E1A$的结果,就能得到消元后的系数矩阵。
上面这个矩阵第一行$[1 0 0]$的意思就是我们只取第一行的方程,而第二行$[0 0 1]$的意思是只取第三个方程,而第三行$[0 1 0]$表示只取第二个方程。
我们先让$E1$左乘$A$,然后再让$E2$左乘$E1A$的结果,就能得到消元后的系数矩阵。
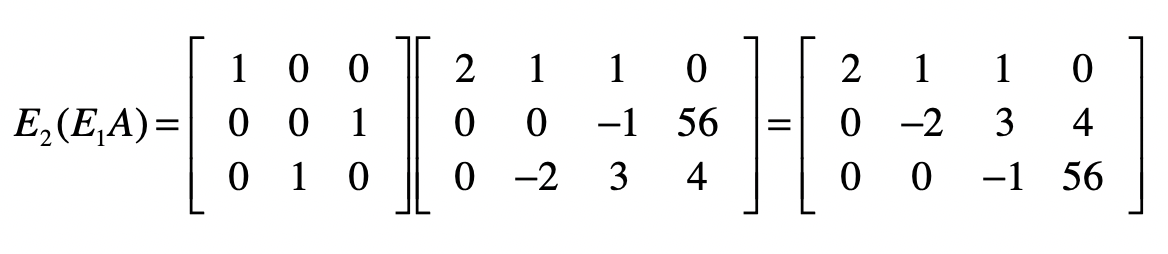 我们把$E1$点乘$E2$的结果记作$E3$,并把$E3$称为消元矩阵。
我们把$E1$点乘$E2$的结果记作$E3$,并把$E3$称为消元矩阵。
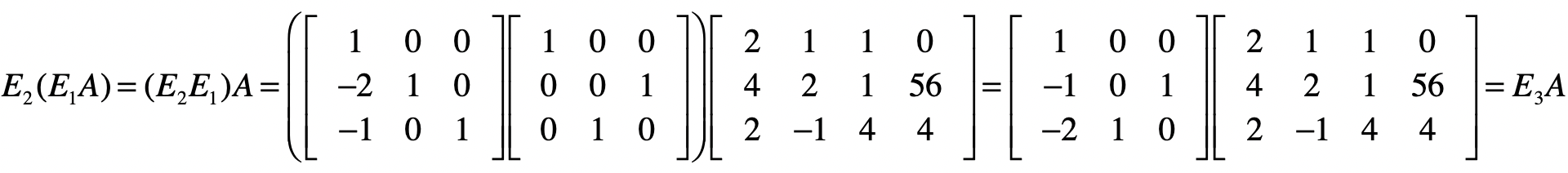
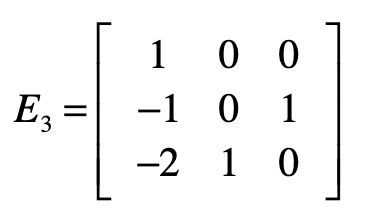 对于目前的结果矩阵来说,除了最后一列,它已经变成了一个上三角矩阵,也就是说消元步骤完成。接下来,我们要使得最后一列之外的部分变成一个单位矩阵,就能得到最终的方程组解。和消元不同的是,我们将从最后一行开始。对于最后一个方程,我们只需要把所有系数取反就行了,所以会使用下面这个矩阵$S1$实现。
对于目前的结果矩阵来说,除了最后一列,它已经变成了一个上三角矩阵,也就是说消元步骤完成。接下来,我们要使得最后一列之外的部分变成一个单位矩阵,就能得到最终的方程组解。和消元不同的是,我们将从最后一行开始。对于最后一个方程,我们只需要把所有系数取反就行了,所以会使用下面这个矩阵$S1$实现。
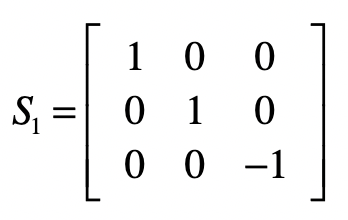
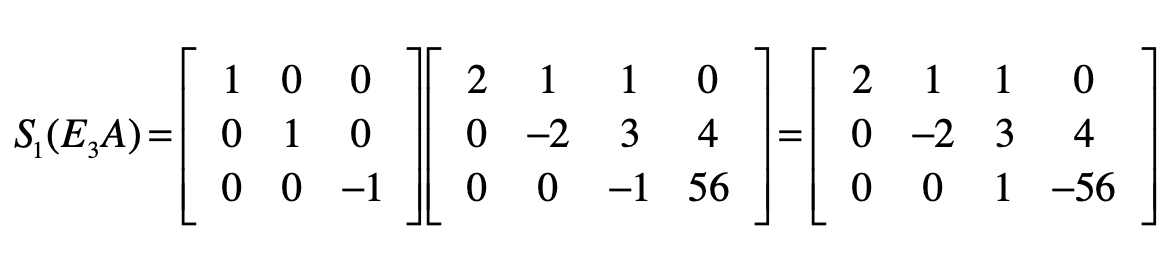 接下来要去掉第二个方程中的$x_3$,我们要把第二个方程减去3倍的第三个方程,然后除以-2。首先是减去3倍的第三个方程。
接下来要去掉第二个方程中的$x_3$,我们要把第二个方程减去3倍的第三个方程,然后除以-2。首先是减去3倍的第三个方程。
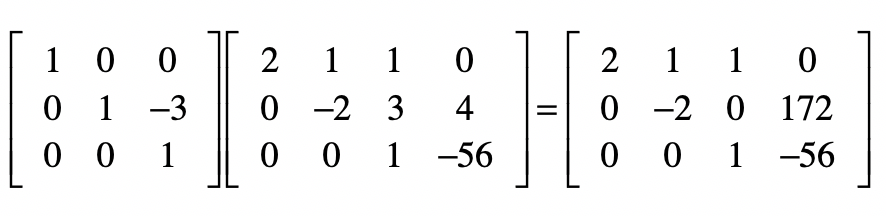 然后把第二个方程除以-2。
然后把第二个方程除以-2。
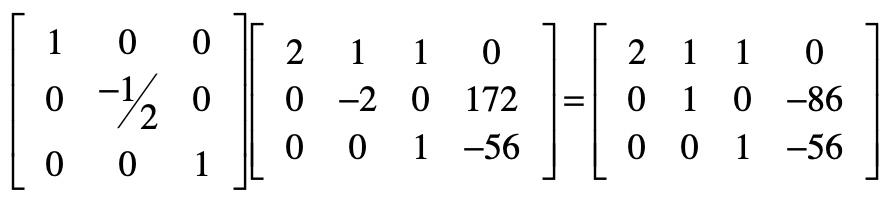 最后,对于第一个方程,我们要把第一个方程减去第二个和第三个方程,最后除以2,我把这几步合并了,并列在下方。
最后,对于第一个方程,我们要把第一个方程减去第二个和第三个方程,最后除以2,我把这几步合并了,并列在下方。
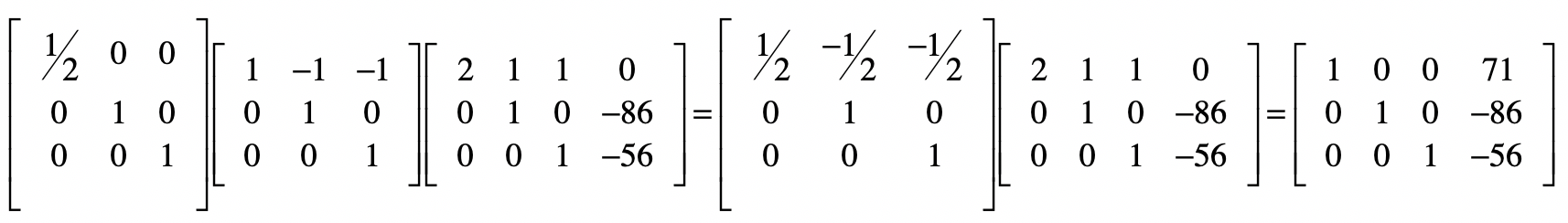 最终,结果矩阵的最后一列就是方程组的解。我们把回代部分的矩阵,都点乘起来。
最终,结果矩阵的最后一列就是方程组的解。我们把回代部分的矩阵,都点乘起来。
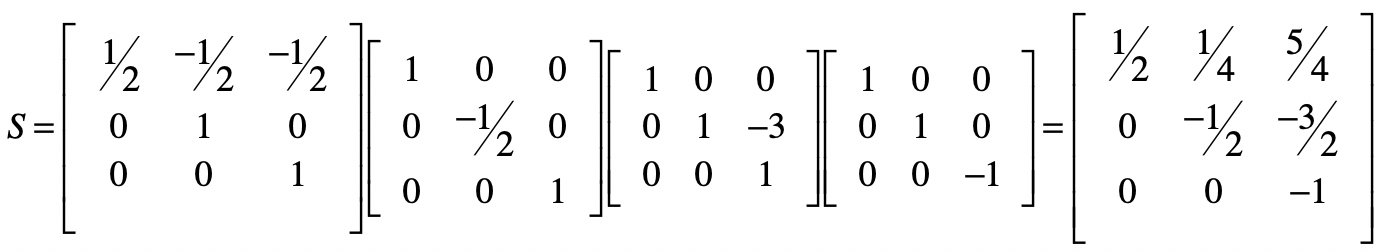 而消元矩阵$E3$为:
而消元矩阵$E3$为:
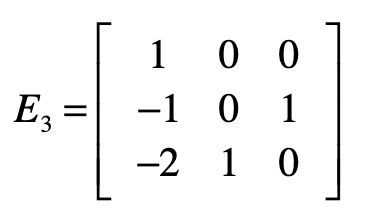 我们可以让矩阵$S$左乘矩阵$E3$,就会得到下面的结果。
我们可以让矩阵$S$左乘矩阵$E3$,就会得到下面的结果。
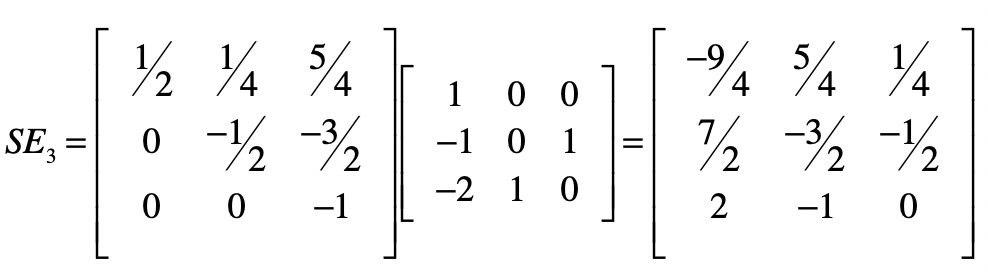 我们把这个矩阵记作$SE$,把乘以最初的系数矩阵$B$,就得到了一个单位矩阵。根据逆矩阵的定义,$SE$就是$B$的逆矩阵。换个角度来思考,使用消元法进行线性方程组求解的过程,就是在找系数矩阵的逆矩阵的过程。
## 总结
今天我们一起探讨了求解线性方程组最常见的方法之一,高斯消元法。这个方法主要包含了消元和回代两个步骤。这些步骤都可以使用矩阵的操作来进行。从矩阵的角度来说,消元就是把系数矩阵变为上三角矩阵,而回代是把这个上三角矩阵变为单位矩阵。我们可以直接把用于消元和回代的矩阵,用于由系数和因变量值组成的增广矩阵,并获得最终的方程解。
线性方程组的概念,也是线性回归分析的基础。在线性回归时,我们也能获得由很多观测数据值所组成的方程组。但是,在进行线性回归分析时,方程组的处理方式和普通的方程组求解有一些不同。其中有两个最主要的区别。
第一个区别是,在线性回归分析中,样本数据会告诉我们自变量和因变量的值,要求的是系数。而在线性方程组中,我们已知系数和因变量的值,要求的是自变量的值。
第二个区别是,在线性回归分析中,方程的数量要远远大于自变量的数量,而且我们不要求每个方程式都是完全成立。这里,不要求完全成立的意思是,拟合出来的因变量值可以和样本数据给定的因变量值存在差异,也就允许模型拟合存在误差。模型拟合的概念我在上一模块的总结篇中重点讲解了,所以你应该能理解,模型的拟合不可能100%完美,这和我们求解线性方程组精确解的概念是不同的。
正是因为这两点差异,我们无法直接使用消元法来求解线性回归。下一节,我会来详细解释,如何使用最小二乘法来解决线性回归的问题。
## 思考题
请分别写出下面这个方程组的消元矩阵和回代矩阵,并求出最终的解。
$x_1-2x_2+x_3-4x_4=4$
我们把这个矩阵记作$SE$,把乘以最初的系数矩阵$B$,就得到了一个单位矩阵。根据逆矩阵的定义,$SE$就是$B$的逆矩阵。换个角度来思考,使用消元法进行线性方程组求解的过程,就是在找系数矩阵的逆矩阵的过程。
## 总结
今天我们一起探讨了求解线性方程组最常见的方法之一,高斯消元法。这个方法主要包含了消元和回代两个步骤。这些步骤都可以使用矩阵的操作来进行。从矩阵的角度来说,消元就是把系数矩阵变为上三角矩阵,而回代是把这个上三角矩阵变为单位矩阵。我们可以直接把用于消元和回代的矩阵,用于由系数和因变量值组成的增广矩阵,并获得最终的方程解。
线性方程组的概念,也是线性回归分析的基础。在线性回归时,我们也能获得由很多观测数据值所组成的方程组。但是,在进行线性回归分析时,方程组的处理方式和普通的方程组求解有一些不同。其中有两个最主要的区别。
第一个区别是,在线性回归分析中,样本数据会告诉我们自变量和因变量的值,要求的是系数。而在线性方程组中,我们已知系数和因变量的值,要求的是自变量的值。
第二个区别是,在线性回归分析中,方程的数量要远远大于自变量的数量,而且我们不要求每个方程式都是完全成立。这里,不要求完全成立的意思是,拟合出来的因变量值可以和样本数据给定的因变量值存在差异,也就允许模型拟合存在误差。模型拟合的概念我在上一模块的总结篇中重点讲解了,所以你应该能理解,模型的拟合不可能100%完美,这和我们求解线性方程组精确解的概念是不同的。
正是因为这两点差异,我们无法直接使用消元法来求解线性回归。下一节,我会来详细解释,如何使用最小二乘法来解决线性回归的问题。
## 思考题
请分别写出下面这个方程组的消元矩阵和回代矩阵,并求出最终的解。
$x_1-2x_2+x_3-4x_4=4$