13 KiB
通过IP地址来查找IP归属地的功能,不知道你有没有用过?没用过也没关系,你现在可以打开百度,在搜索框里随便输一个IP地址,就会看到它的归属地。
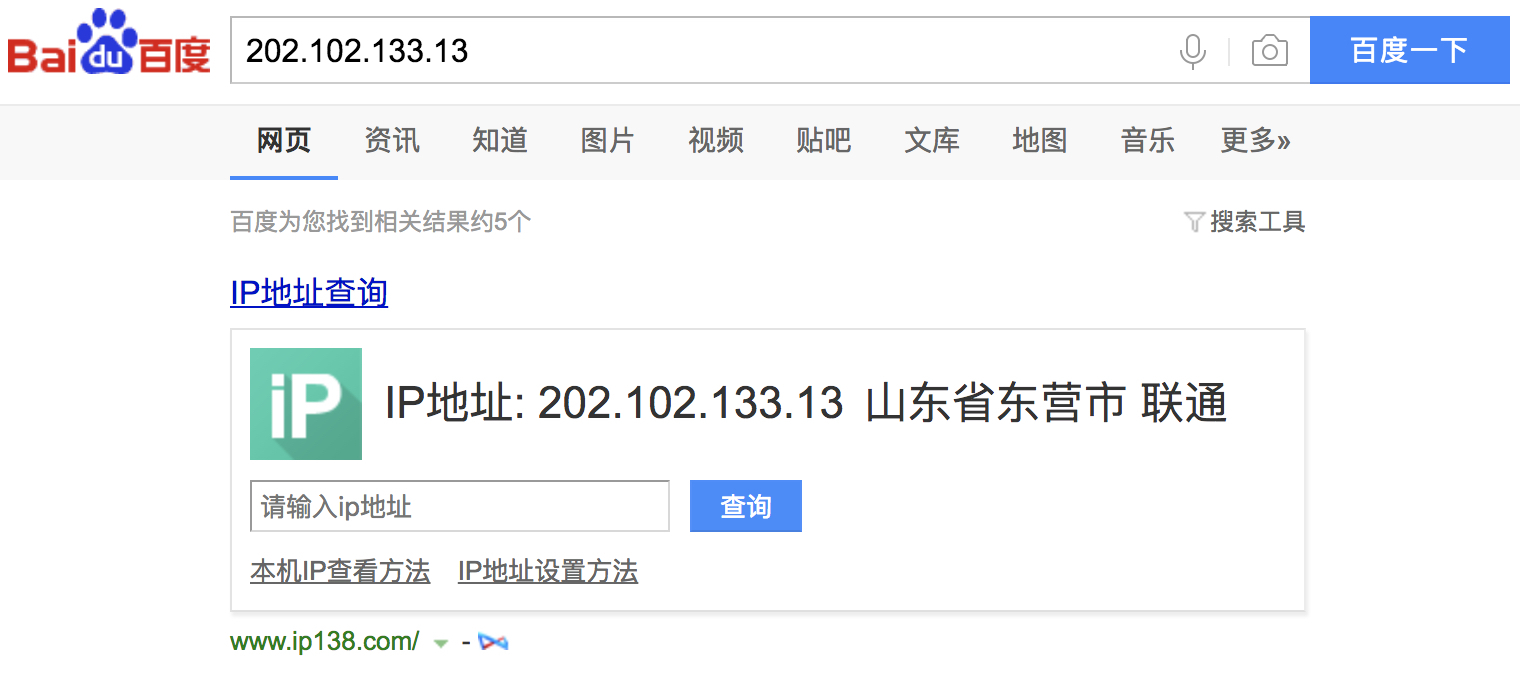
这个功能并不复杂,它是通过维护一个很大的IP地址库来实现的。地址库中包括IP地址范围和归属地的对应关系。
当我们想要查询202.102.133.13这个IP地址的归属地时,我们就在地址库中搜索,发现这个IP地址落在[202.102.133.0, 202.102.133.255]这个地址范围内,那我们就可以将这个IP地址范围对应的归属地“山东东营市”显示给用户了。
[202.102.133.0, 202.102.133.255] 山东东营市
[202.102.135.0, 202.102.136.255] 山东烟台
[202.102.156.34, 202.102.157.255] 山东青岛
[202.102.48.0, 202.102.48.255] 江苏宿迁
[202.102.49.15, 202.102.51.251] 江苏泰州
[202.102.56.0, 202.102.56.255] 江苏连云港
现在我的问题是,在庞大的地址库中逐一比对IP地址所在的区间,是非常耗时的。假设我们有12万条这样的IP区间与归属地的对应关系,如何快速定位出一个IP地址的归属地呢?
是不是觉得比较难?不要紧,等学完今天的内容,你就会发现这个问题其实很简单。
上一节我讲了二分查找的原理,并且介绍了最简单的一种二分查找的代码实现。今天我们来讲几种二分查找的变形问题。
不知道你有没有听过这样一个说法:“十个二分九个错”。二分查找虽然原理极其简单,但是想要写出没有Bug的二分查找并不容易。
唐纳德·克努特(Donald E.Knuth)在《计算机程序设计艺术》的第3卷《排序和查找》中说到:“尽管第一个二分查找算法于1946年出现,然而第一个完全正确的二分查找算法实现直到1962年才出现。”
你可能会说,我们上一节学的二分查找的代码实现并不难写啊。那是因为上一节讲的只是二分查找中最简单的一种情况,在不存在重复元素的有序数组中,查找值等于给定值的元素。最简单的二分查找写起来确实不难,但是,二分查找的变形问题就没那么好写了。
二分查找的变形问题很多,我只选择几个典型的来讲解,其他的你可以借助我今天讲的思路自己来分析。

需要特别说明一点,为了简化讲解,今天的内容,我都以数据是从小到大排列为前提,如果你要处理的数据是从大到小排列的,解决思路也是一样的。同时,我希望你最好先自己动手试着写一下这4个变形问题,然后再看我的讲述,这样你就会对我说的“二分查找比较难写”有更加深的体会了。
变体一:查找第一个值等于给定值的元素
上一节中的二分查找是最简单的一种,即有序数据集合中不存在重复的数据,我们在其中查找值等于某个给定值的数据。如果我们将这个问题稍微修改下,有序数据集合中存在重复的数据,我们希望找到第一个值等于给定值的数据,这样之前的二分查找代码还能继续工作吗?
比如下面这样一个有序数组,其中,a[5],a[6],a[7]的值都等于8,是重复的数据。我们希望查找第一个等于8的数据,也就是下标是5的元素。
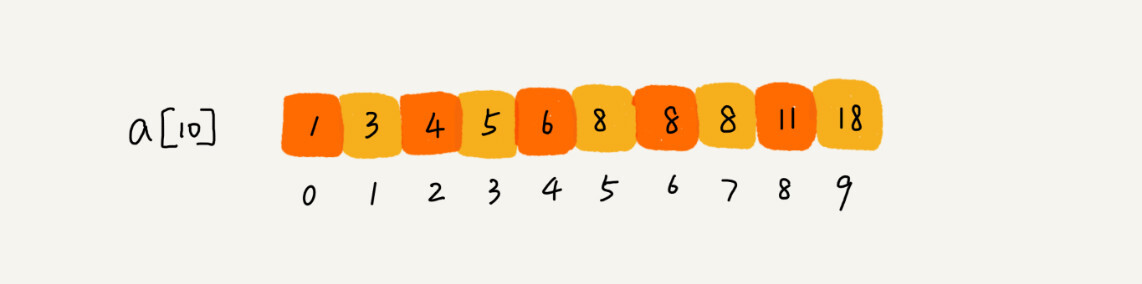
如果我们用上一节课讲的二分查找的代码实现,首先拿8与区间的中间值a[4]比较,8比6大,于是在下标5到9之间继续查找。下标5和9的中间位置是下标7,a[7]正好等于8,所以代码就返回了。
尽管a[7]也等于8,但它并不是我们想要找的第一个等于8的元素,因为第一个值等于8的元素是数组下标为5的元素。我们上一节讲的二分查找代码就无法处理这种情况了。所以,针对这个变形问题,我们可以稍微改造一下上一节的代码。
100个人写二分查找就会有100种写法。网上有很多关于变形二分查找的实现方法,有很多写得非常简洁,比如下面这个写法。但是,尽管简洁,理解起来却非常烧脑,也很容易写错。
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
high = mid - 1;
} else {
low = mid + 1;
}
}
if (low < n && a[low]==value) return low;
else return -1;
}
看完这个实现之后,你是不是觉得很不好理解?如果你只是死记硬背这个写法,我敢保证,过不了几天,你就会全都忘光,再让你写,90%的可能会写错。所以,我换了一种实现方法,你看看是不是更容易理解呢?
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == 0) || (a[mid - 1] != value)) return mid;
else high = mid - 1;
}
}
return -1;
}
我来稍微解释一下这段代码。a[mid]跟要查找的value的大小关系有三种情况:大于、小于、等于。对于a[mid]>value的情况,我们需要更新high= mid-1;对于a[mid]<value的情况,我们需要更新low=mid+1。这两点都很好理解。那当a[mid]=value的时候应该如何处理呢?
如果我们查找的是任意一个值等于给定值的元素,当a[mid]等于要查找的值时,a[mid]就是我们要找的元素。但是,如果我们求解的是第一个值等于给定值的元素,当a[mid]等于要查找的值时,我们就需要确认一下这个a[mid]是不是第一个值等于给定值的元素。
我们重点看第11行代码。如果mid等于0,那这个元素已经是数组的第一个元素,那它肯定是我们要找的;如果mid不等于0,但a[mid]的前一个元素a[mid-1]不等于value,那也说明a[mid]就是我们要找的第一个值等于给定值的元素。
如果经过检查之后发现a[mid]前面的一个元素a[mid-1]也等于value,那说明此时的a[mid]肯定不是我们要查找的第一个值等于给定值的元素。那我们就更新high=mid-1,因为要找的元素肯定出现在[low, mid-1]之间。
对比上面的两段代码,是不是下面那种更好理解?实际上,很多人都觉得变形的二分查找很难写,主要原因是太追求第一种那样完美、简洁的写法。而对于我们做工程开发的人来说,代码易读懂、没Bug,其实更重要,所以我觉得第二种写法更好。
变体二:查找最后一个值等于给定值的元素
前面的问题是查找第一个值等于给定值的元素,我现在把问题稍微改一下,查找最后一个值等于给定值的元素,又该如何做呢?
如果你掌握了前面的写法,那这个问题你应该很轻松就能解决。你可以先试着实现一下,然后跟我写的对比一下。
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
else low = mid + 1;
}
}
return -1;
}
我们还是重点看第11行代码。如果a[mid]这个元素已经是数组中的最后一个元素了,那它肯定是我们要找的;如果a[mid]的后一个元素a[mid+1]不等于value,那也说明a[mid]就是我们要找的最后一个值等于给定值的元素。
如果我们经过检查之后,发现a[mid]后面的一个元素a[mid+1]也等于value,那说明当前的这个a[mid]并不是最后一个值等于给定值的元素。我们就更新low=mid+1,因为要找的元素肯定出现在[mid+1, high]之间。
变体三:查找第一个大于等于给定值的元素
现在我们再来看另外一类变形问题。在有序数组中,查找第一个大于等于给定值的元素。比如,数组中存储的这样一个序列:3,4,6,7,10。如果查找第一个大于等于5的元素,那就是6。
实际上,实现的思路跟前面的那两种变形问题的实现思路类似,代码写起来甚至更简洁。
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
if ((mid == 0) || (a[mid - 1] < value)) return mid;
else high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}
如果a[mid]小于要查找的值value,那要查找的值肯定在[mid+1, high]之间,所以,我们更新low=mid+1。
对于a[mid]大于等于给定值value的情况,我们要先看下这个a[mid]是不是我们要找的第一个值大于等于给定值的元素。如果a[mid]前面已经没有元素,或者前面一个元素小于要查找的值value,那a[mid]就是我们要找的元素。这段逻辑对应的代码是第7行。
如果a[mid-1]也大于等于要查找的值value,那说明要查找的元素在[low, mid-1]之间,所以,我们将high更新为mid-1。
变体四:查找最后一个小于等于给定值的元素
现在,我们来看最后一种二分查找的变形问题,查找最后一个小于等于给定值的元素。比如,数组中存储了这样一组数据:3,5,6,8,9,10。最后一个小于等于7的元素就是6。是不是有点类似上面那一种?实际上,实现思路也是一样的。
有了前面的基础,你完全可以自己写出来了,所以我就不详细分析了。我把代码贴出来,你可以写完之后对比一下。
public int bsearch7(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else {
if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
else low = mid + 1;
}
}
return -1;
}
解答开篇
好了,现在我们回头来看开篇的问题:如何快速定位出一个IP地址的归属地?
现在这个问题应该很简单了。如果IP区间与归属地的对应关系不经常更新,我们可以先预处理这12万条数据,让其按照起始IP从小到大排序。如何来排序呢?我们知道,IP地址可以转化为32位的整型数。所以,我们可以将起始地址,按照对应的整型值的大小关系,从小到大进行排序。
然后,这个问题就可以转化为我刚讲的第四种变形问题“在有序数组中,查找最后一个小于等于某个给定值的元素”了。
当我们要查询某个IP归属地时,我们可以先通过二分查找,找到最后一个起始IP小于等于这个IP的IP区间,然后,检查这个IP是否在这个IP区间内,如果在,我们就取出对应的归属地显示;如果不在,就返回未查找到。
内容小结
上一节我说过,凡是用二分查找能解决的,绝大部分我们更倾向于用散列表或者二叉查找树。即便是二分查找在内存使用上更节省,但是毕竟内存如此紧缺的情况并不多。那二分查找真的没什么用处了吗?
实际上,上一节讲的求“值等于给定值”的二分查找确实不怎么会被用到,二分查找更适合用在“近似”查找问题,在这类问题上,二分查找的优势更加明显。比如今天讲的这几种变体问题,用其他数据结构,比如散列表、二叉树,就比较难实现了。
变体的二分查找算法写起来非常烧脑,很容易因为细节处理不好而产生Bug,这些容易出错的细节有:终止条件、区间上下界更新方法、返回值选择。所以今天的内容你最好能用自己实现一遍,对锻炼编码能力、逻辑思维、写出Bug free代码,会很有帮助。
课后思考
我们今天讲的都是非常规的二分查找问题,今天的思考题也是一个非常规的二分查找问题。如果有序数组是一个循环有序数组,比如4,5,6,1,2,3。针对这种情况,如何实现一个求“值等于给定值”的二分查找算法呢?
欢迎留言和我分享,我会第一时间给你反馈。