22 KiB
文本编辑器中的查找替换功能,我想你应该不陌生吧?比如,我们在Word中把一个单词统一替换成另一个,用的就是这个功能。你有没有想过,它是怎么实现的呢?
当然,你用上一节讲的BF算法和RK算法,也可以实现这个功能,但是在某些极端情况下,BF算法性能会退化的比较严重,而RK算法需要用到哈希算法,设计一个可以应对各种类型字符的哈希算法并不简单。
对于工业级的软件开发来说,我们希望算法尽可能的高效,并且在极端情况下,性能也不要退化的太严重。那么,对于查找功能是重要功能的软件来说,比如一些文本编辑器,它们的查找功能都是用哪种算法来实现的呢?有没有比BF算法和RK算法更加高效的字符串匹配算法呢?
今天,我们就来学习BM(Boyer-Moore)算法。它是一种非常高效的字符串匹配算法,有实验统计,它的性能是著名的KMP算法的3到4倍**。**BM算法的原理很复杂,比较难懂,学起来会比较烧脑,我会尽量给你讲清楚,同时也希望你做好打硬仗的准备。好,现在我们正式开始!
BM算法的核心思想
我们把模式串和主串的匹配过程,看作模式串在主串中不停地往后滑动。当遇到不匹配的字符时,BF算法和RK算法的做法是,模式串往后滑动一位,然后从模式串的第一个字符开始重新匹配。我举个例子解释一下,你可以看我画的这幅图。
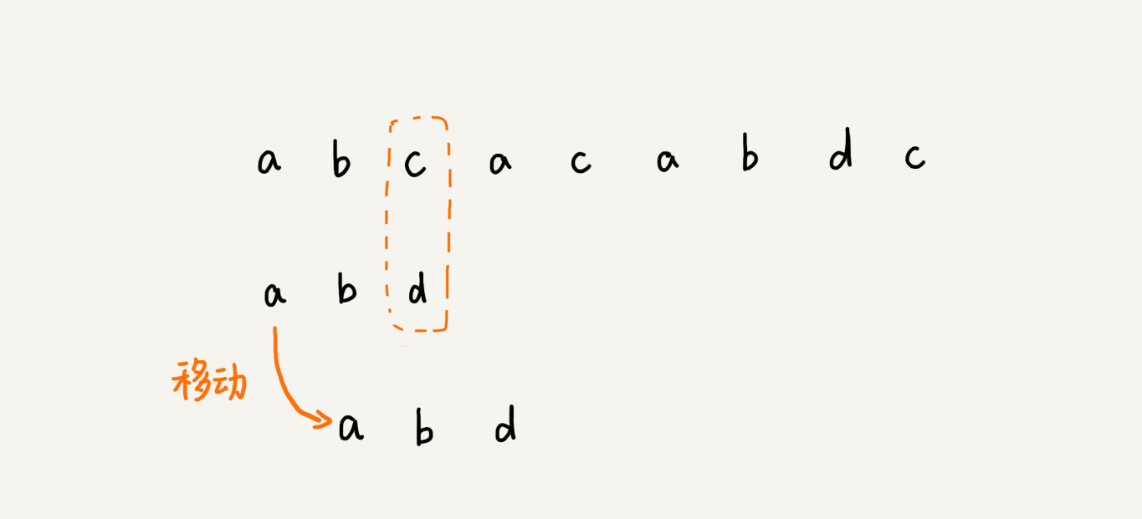
在这个例子里,主串中的c,在模式串中是不存在的,所以,模式串向后滑动的时候,只要c与模式串没有重合,肯定无法匹配。所以,我们可以一次性把模式串往后多滑动几位,把模式串移动到c的后面。
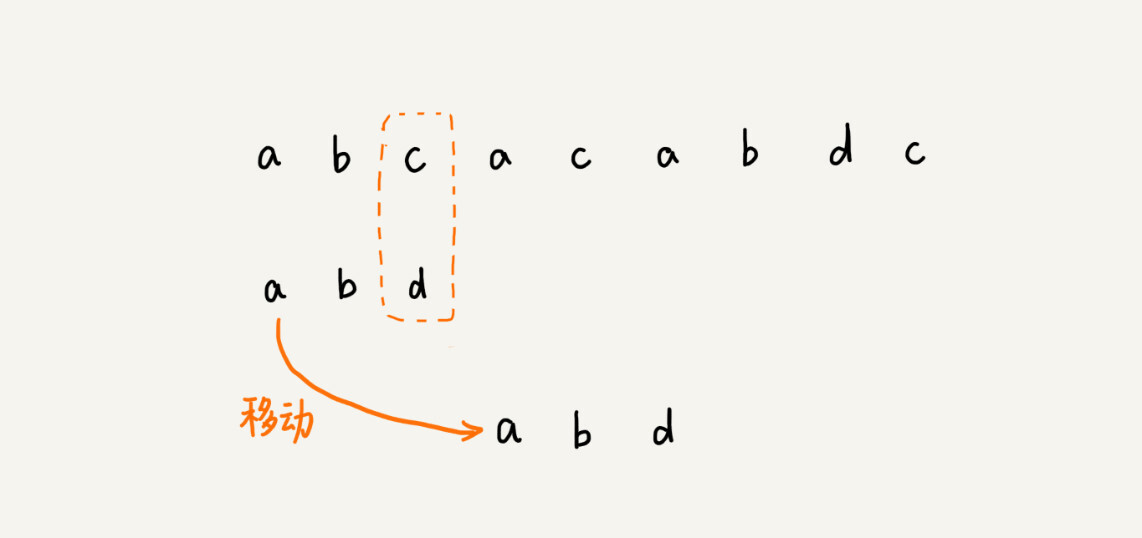
由现象找规律,你可以思考一下,当遇到不匹配的字符时,有什么固定的规律,可以将模式串往后多滑动几位呢?这样一次性往后滑动好几位,那匹配的效率岂不是就提高了?
我们今天要讲的BM算法,本质上其实就是在寻找这种规律。借助这种规律,在模式串与主串匹配的过程中,当模式串和主串某个字符不匹配的时候,能够跳过一些肯定不会匹配的情况,将模式串往后多滑动几位。
BM算法原理分析
BM算法包含两部分,分别是坏字符规则(bad character rule)和好后缀规则(good suffix shift)。我们下面依次来看,这两个规则分别都是怎么工作的。
1.坏字符规则
前面两节讲的算法,在匹配的过程中,我们都是按模式串的下标从小到大的顺序,依次与主串中的字符进行匹配的。这种匹配顺序比较符合我们的思维习惯,而BM算法的匹配顺序比较特别,它是按照模式串下标从大到小的顺序,倒着匹配的。我画了一张图,你可以看下。
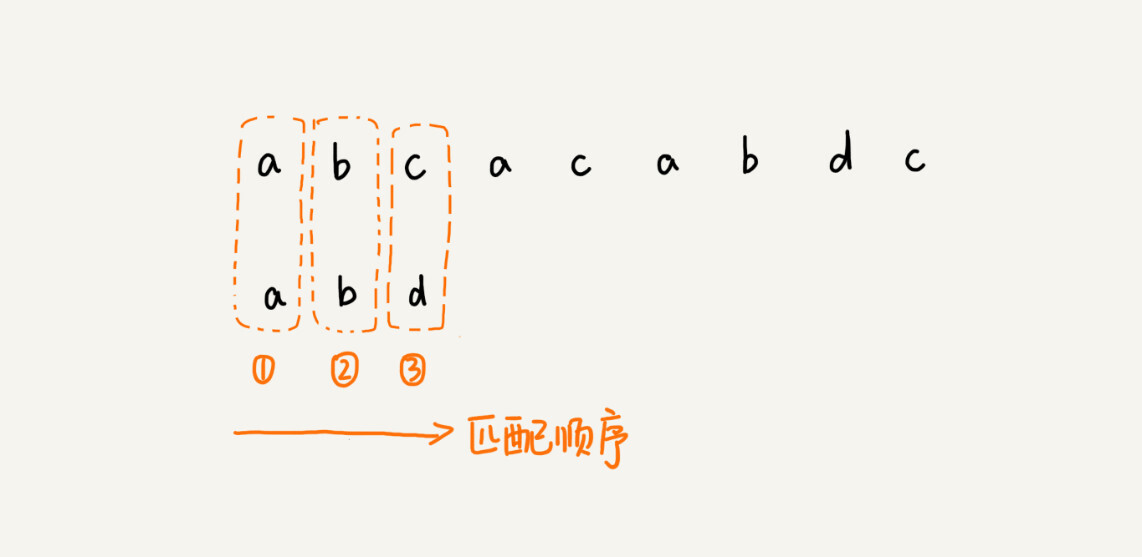
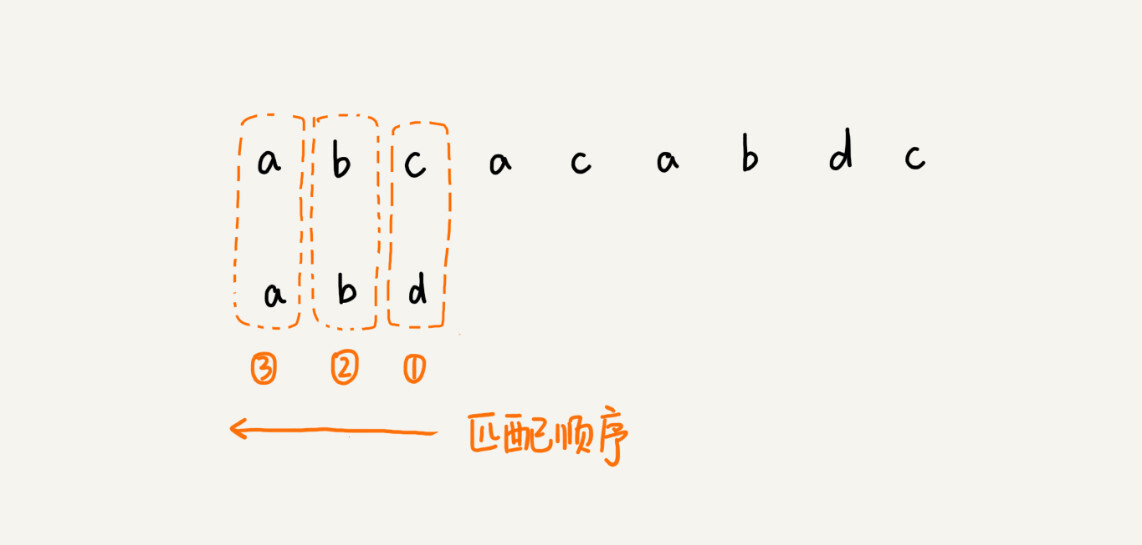
从模式串的末尾往前倒着匹配,当发现某个字符没法匹配的时候,我们把这个没有匹配的字符叫作坏字符(主串中的字符)。
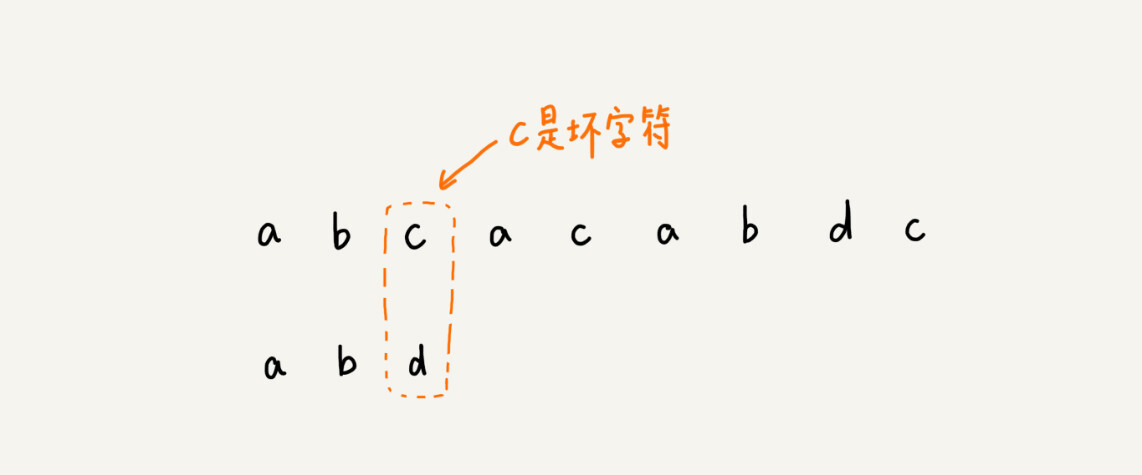
我们拿坏字符c在模式串中查找,发现模式串中并不存在这个字符,也就是说,字符c与模式串中的任何字符都不可能匹配。这个时候,我们可以将模式串直接往后滑动三位,将模式串滑动到c后面的位置,再从模式串的末尾字符开始比较。
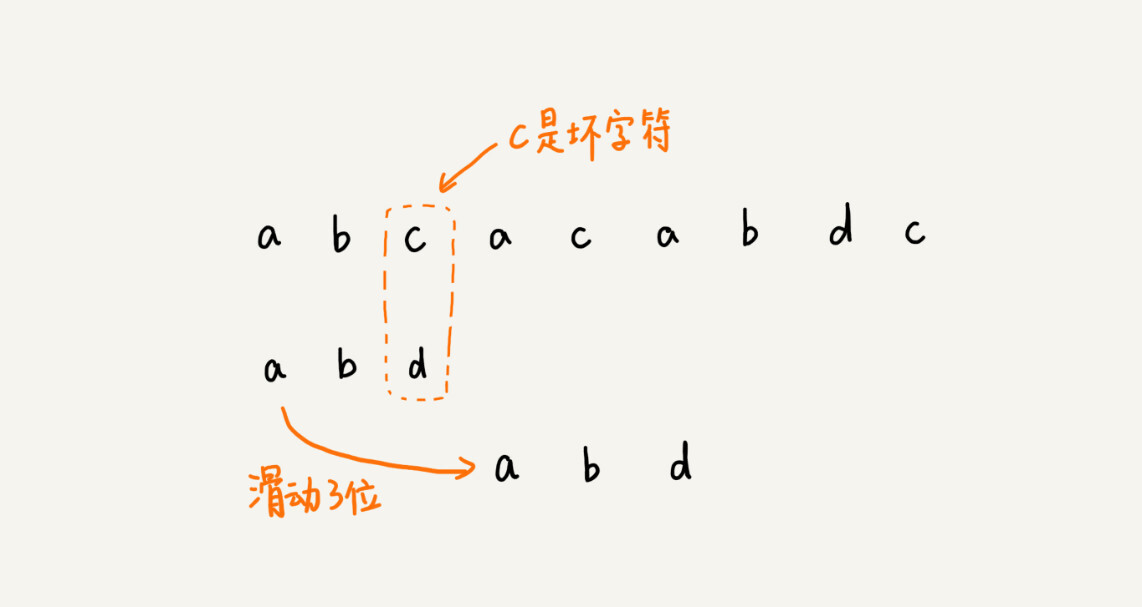
这个时候,我们发现,模式串中最后一个字符d,还是无法跟主串中的a匹配,这个时候,还能将模式串往后滑动三位吗?答案是不行的。因为这个时候,坏字符a在模式串中是存在的,模式串中下标是0的位置也是字符a。这种情况下,我们可以将模式串往后滑动两位,让两个a上下对齐,然后再从模式串的末尾字符开始,重新匹配。

第一次不匹配的时候,我们滑动了三位,第二次不匹配的时候,我们将模式串后移两位,那具体滑动多少位,到底有没有规律呢?
当发生不匹配的时候,我们把坏字符对应的模式串中的字符下标记作si。如果坏字符在模式串中存在,我们把这个坏字符在模式串中的下标记作xi。如果不存在,我们把xi记作-1。那模式串往后移动的位数就等于si-xi。(注意,我这里说的下标,都是字符在模式串的下标)。
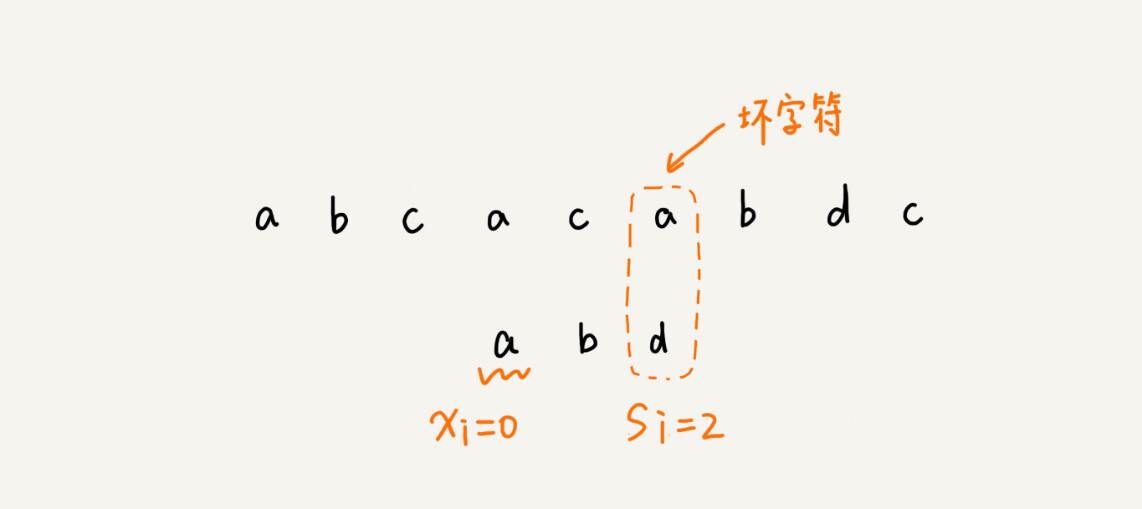
这里我要特别说明一点,如果坏字符在模式串里多处出现,那我们在计算xi的时候,选择最靠后的那个,因为这样不会让模式串滑动过多,导致本来可能匹配的情况被滑动略过。
利用坏字符规则,BM算法在最好情况下的时间复杂度非常低,是O(n/m)。比如,主串是aaabaaabaaabaaab,模式串是aaaa。每次比对,模式串都可以直接后移四位,所以,匹配具有类似特点的模式串和主串的时候,BM算法非常高效。
不过,单纯使用坏字符规则还是不够的。因为根据si-xi计算出来的移动位数,有可能是负数,比如主串是aaaaaaaaaaaaaaaa,模式串是baaa。不但不会向后滑动模式串,还有可能倒退。所以,BM算法还需要用到“好后缀规则”。
2.好后缀规则
好后缀规则实际上跟坏字符规则的思路很类似。你看我下面这幅图。当模式串滑动到图中的位置的时候,模式串和主串有2个字符是匹配的,倒数第3个字符发生了不匹配的情况。
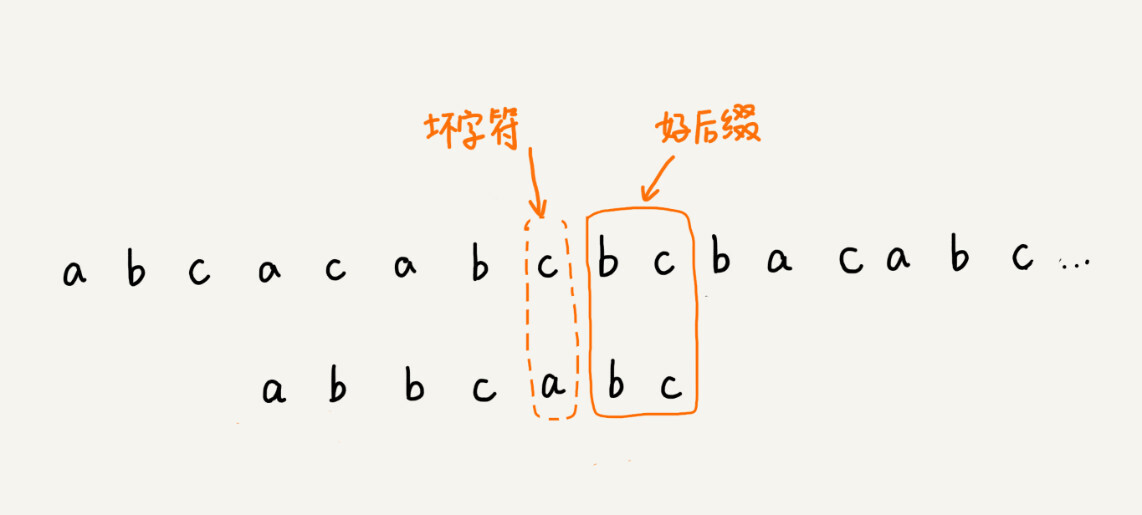
这个时候该如何滑动模式串呢?当然,我们还可以利用坏字符规则来计算模式串的滑动位数,不过,我们也可以使用好后缀处理规则。两种规则到底如何选择,我稍后会讲。抛开这个问题,现在我们来看,好后缀规则是怎么工作的?
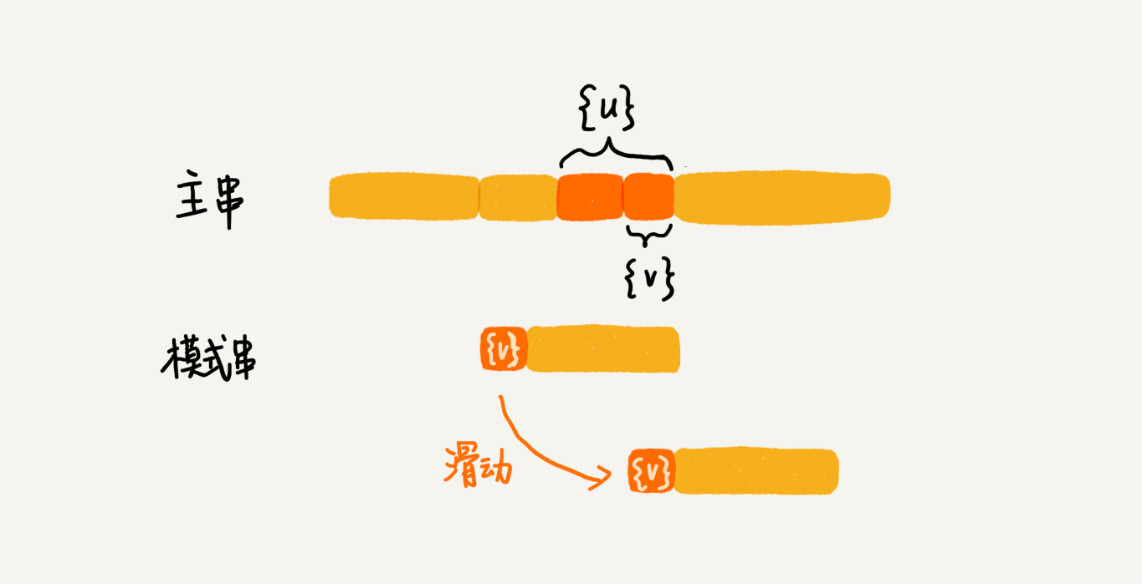
我们把已经匹配的bc叫作好后缀,记作{u}。我们拿它在模式串中查找,如果找到了另一个跟{u}相匹配的子串{u*},那我们就将模式串滑动到子串{u*}与主串中{u}对齐的位置。
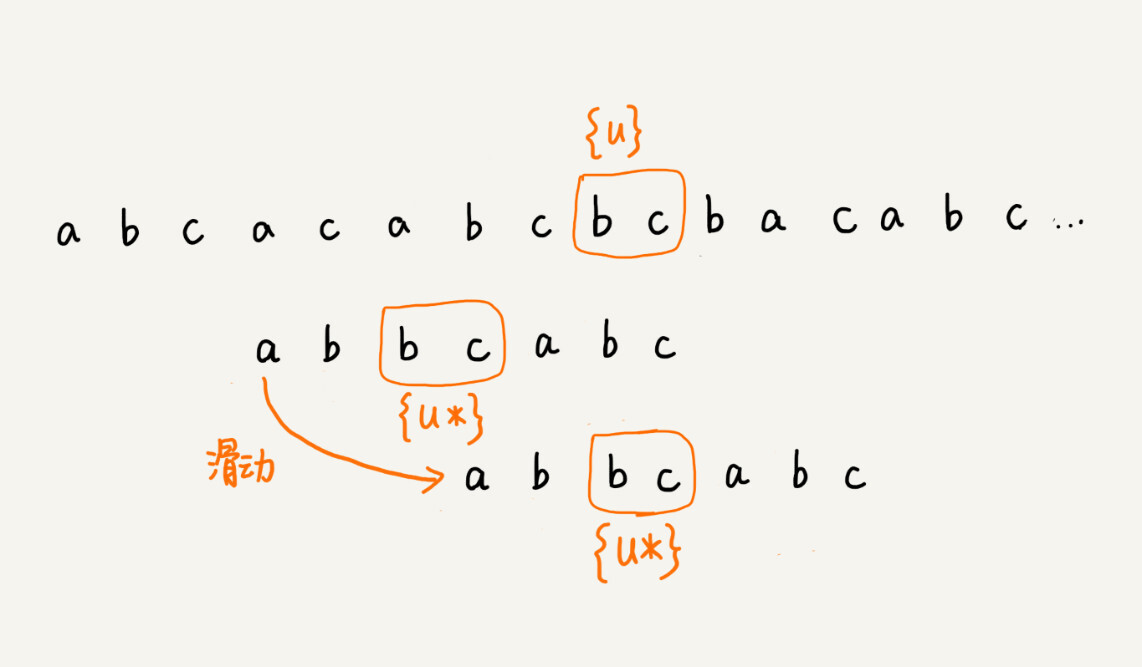
如果在模式串中找不到另一个等于{u}的子串,我们就直接将模式串,滑动到主串中{u}的后面,因为之前的任何一次往后滑动,都没有匹配主串中{u}的情况。
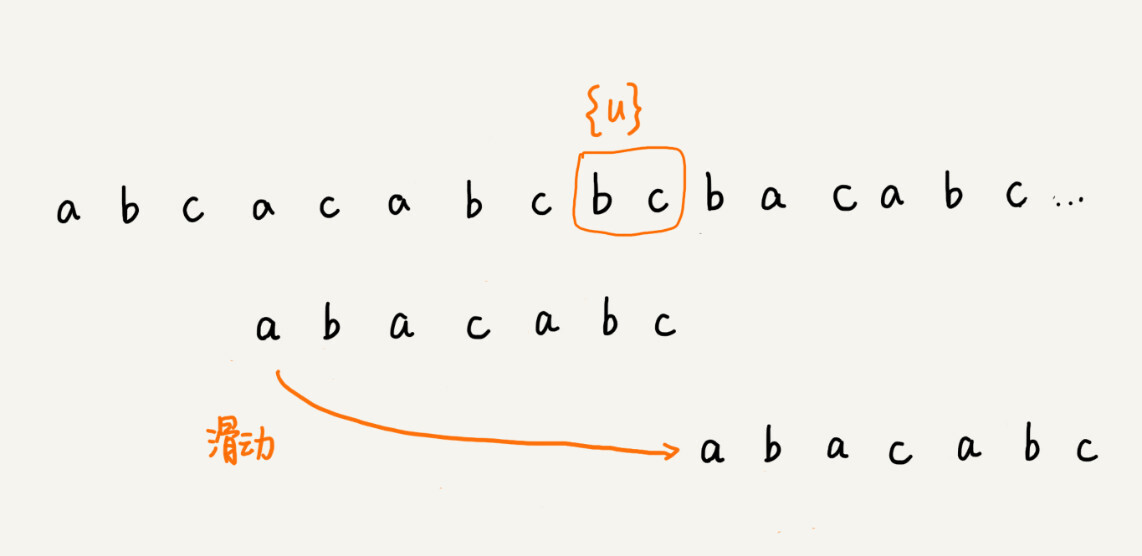
不过,当模式串中不存在等于{u}的子串时,我们直接将模式串滑动到主串{u}的后面。这样做是否有点太过头呢?我们来看下面这个例子。这里面bc是好后缀,尽管在模式串中没有另外一个相匹配的子串{u*},但是如果我们将模式串移动到好后缀的后面,如图所示,那就会错过模式串和主串可以匹配的情况。
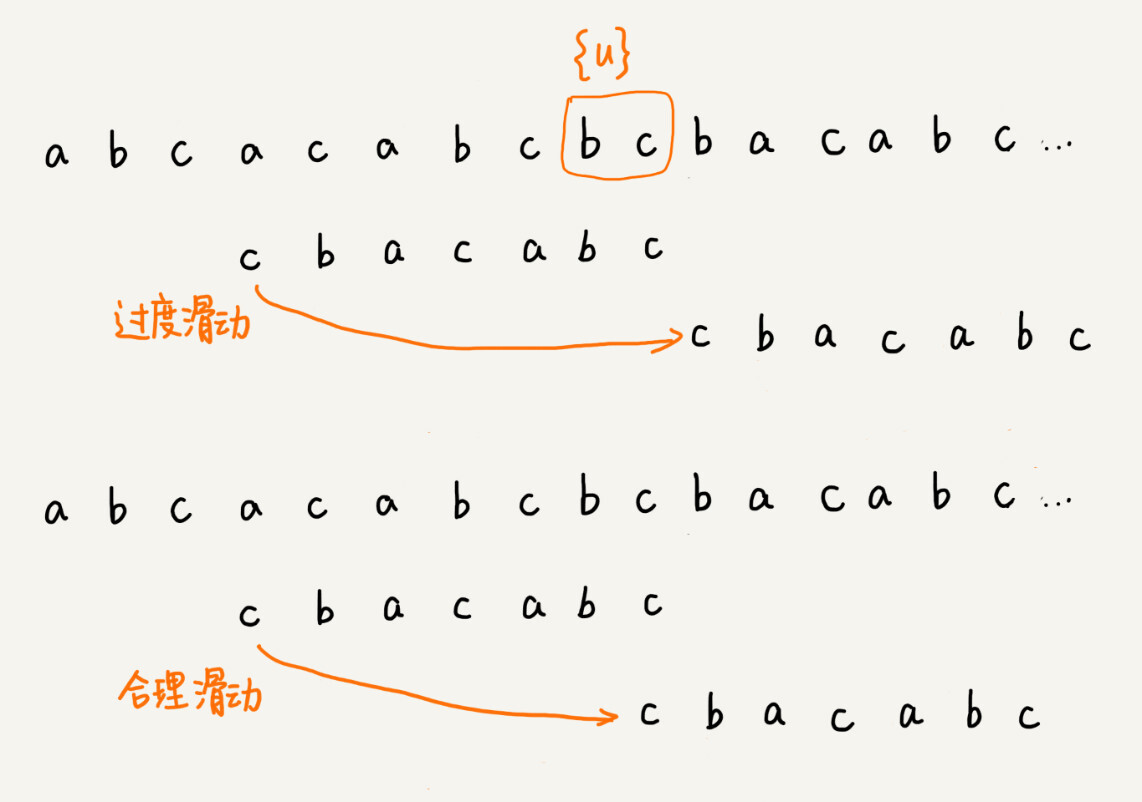
如果好后缀在模式串中不存在可匹配的子串,那在我们一步一步往后滑动模式串的过程中,只要主串中的{u}与模式串有重合,那肯定就无法完全匹配。但是当模式串滑动到前缀与主串中{u}的后缀有部分重合的时候,并且重合的部分相等的时候,就有可能会存在完全匹配的情况。
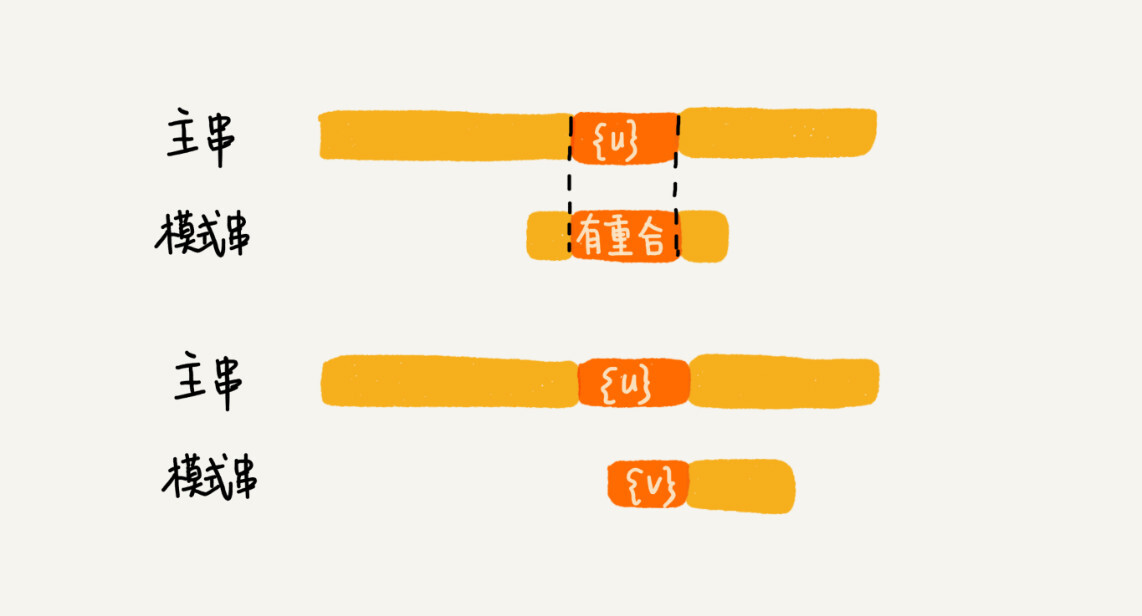
所以,针对这种情况,我们不仅要看好后缀在模式串中,是否有另一个匹配的子串,我们还要考察好后缀的后缀子串,是否存在跟模式串的前缀子串匹配的。
所谓某个字符串s的后缀子串,就是最后一个字符跟s对齐的子串,比如abc的后缀子串就包括c, bc。所谓前缀子串,就是起始字符跟s对齐的子串,比如abc的前缀子串有a,ab。我们从好后缀的后缀子串中,找一个最长的并且能跟模式串的前缀子串匹配的,假设是{v},然后将模式串滑动到如图所示的位置。
坏字符和好后缀的基本原理都讲完了,我现在回答一下前面那个问题。当模式串和主串中的某个字符不匹配的时候,如何选择用好后缀规则还是坏字符规则,来计算模式串往后滑动的位数?
我们可以分别计算好后缀和坏字符往后滑动的位数,然后取两个数中最大的,作为模式串往后滑动的位数。这种处理方法还可以避免我们前面提到的,根据坏字符规则,计算得到的往后滑动的位数,有可能是负数的情况。
BM算法代码实现
学习完了基本原理,我们再来看,如何实现BM算法?
“坏字符规则”本身不难理解。当遇到坏字符时,要计算往后移动的位数si-xi,其中xi的计算是重点,我们如何求得xi呢?或者说,如何查找坏字符在模式串中出现的位置呢?
如果我们拿坏字符,在模式串中顺序遍历查找,这样就会比较低效,势必影响这个算法的性能。有没有更加高效的方式呢?我们之前学的散列表,这里可以派上用场了。我们可以将模式串中的每个字符及其下标都存到散列表中。这样就可以快速找到坏字符在模式串的位置下标了。
关于这个散列表,我们只实现一种最简单的情况,假设字符串的字符集不是很大,每个字符长度是1字节,我们用大小为256的数组,来记录每个字符在模式串中出现的位置。数组的下标对应字符的ASCII码值,数组中存储这个字符在模式串中出现的位置。
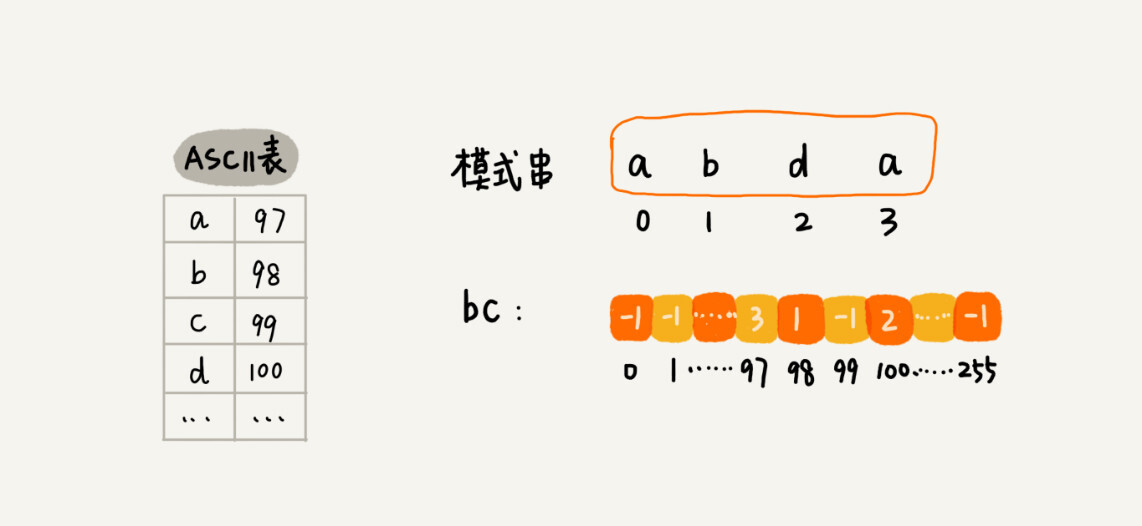
如果将上面的过程翻译成代码,就是下面这个样子。其中,变量b是模式串,m是模式串的长度,bc表示刚刚讲的散列表。
private static final int SIZE = 256; // 全局变量或成员变量
private void generateBC(char[] b, int m, int[] bc) {
for (int i = 0; i < SIZE; ++i) {
bc[i] = -1; // 初始化bc
}
for (int i = 0; i < m; ++i) {
int ascii = (int)b[i]; // 计算b[i]的ASCII值
bc[ascii] = i;
}
}
掌握了坏字符规则之后,我们先把BM算法代码的大框架写好,先不考虑好后缀规则,仅用坏字符规则,并且不考虑si-xi计算得到的移动位数可能会出现负数的情况。
public int bm(char[] a, int n, char[] b, int m) {
int[] bc = new int[SIZE]; // 记录模式串中每个字符最后出现的位置
generateBC(b, m, bc); // 构建坏字符哈希表
int i = 0; // i表示主串与模式串对齐的第一个字符
while (i <= n - m) {
int j;
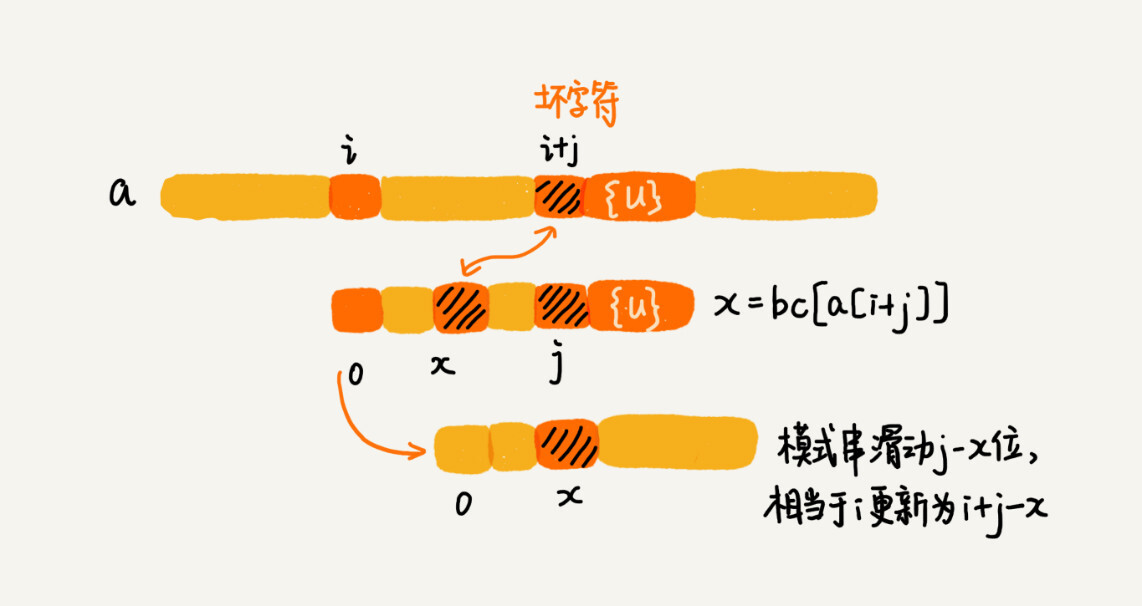
for (j = m - 1; j >= 0; --j) { // 模式串从后往前匹配
if (a[i+j] != b[j]) break; // 坏字符对应模式串中的下标是j
}
if (j < 0) {
return i; // 匹配成功,返回主串与模式串第一个匹配的字符的位置
}
// 这里等同于将模式串往后滑动j-bc[(int)a[i+j]]位
i = i + (j - bc[(int)a[i+j]]);
}
return -1;
}
代码里的注释已经很详细了,我就不再赘述了。不过,为了你方便理解,我画了一张图,将其中的一些关键变量标注在上面了,结合着图,代码应该更好理解。
至此,我们已经实现了包含坏字符规则的框架代码,只剩下往框架代码中填充好后缀规则了。现在,我们就来看看,如何实现好后缀规则。它的实现要比坏字符规则复杂一些。
在讲实现之前,我们先简单回顾一下,前面讲过好后缀的处理规则中最核心的内容:
在不考虑效率的情况下,这两个操作都可以用很“暴力”的匹配查找方式解决。但是,如果想要BM算法的效率很高,这部分就不能太低效。如何来做呢?
因为好后缀也是模式串本身的后缀子串,所以,我们可以在模式串和主串正式匹配之前,通过预处理模式串,预先计算好模式串的每个后缀子串,对应的另一个可匹配子串的位置。这个预处理过程比较有技巧,很不好懂,应该是这节最难懂的内容了,你要认真多读几遍。
我们先来看,**如何表示模式串中不同的后缀子串呢?**因为后缀子串的最后一个字符的位置是固定的,下标为m-1,我们只需要记录长度就可以了。通过长度,我们可以确定一个唯一的后缀子串。
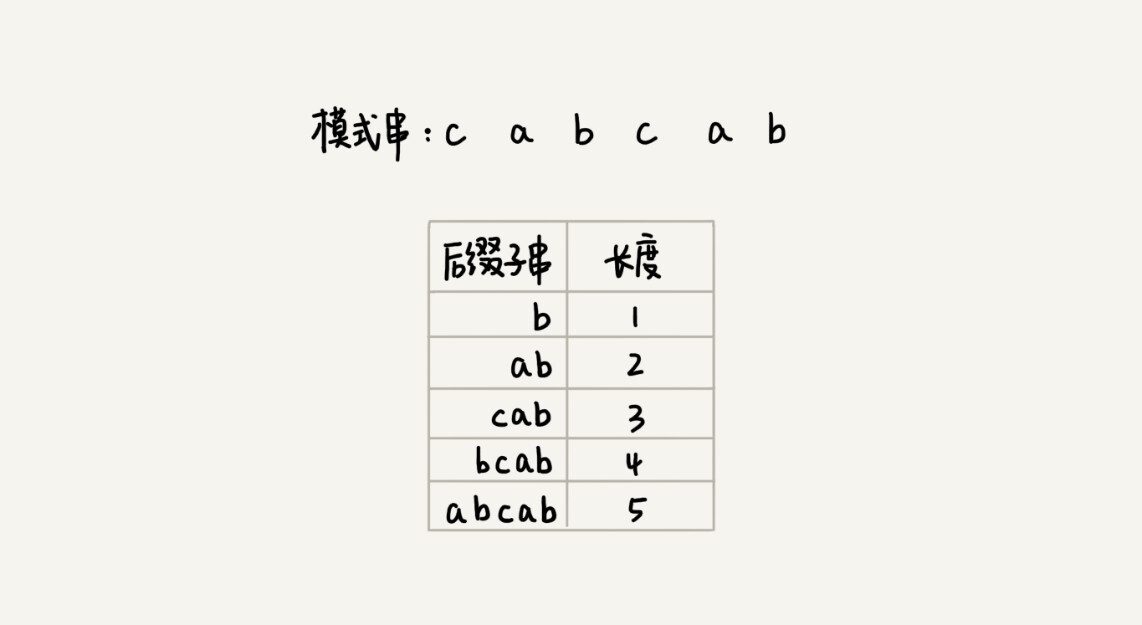
现在,我们要引入最关键的变量suffix数组。suffix数组的下标k,表示后缀子串的长度,下标对应的数组值存储的是,在模式串中跟好后缀{u}相匹配的子串{u*}的起始下标值。这句话不好理解,我举一个例子。

但是,如果模式串中有多个(大于1个)子串跟后缀子串{u}匹配,那suffix数组中该存储哪一个子串的起始位置呢?为了避免模式串往后滑动得过头了,我们肯定要存储模式串中最靠后的那个子串的起始位置,也就是下标最大的那个子串的起始位置。不过,这样处理就足够了吗?
实际上,仅仅是选最靠后的子串片段来存储是不够的。我们再回忆一下好后缀规则。
我们不仅要在模式串中,查找跟好后缀匹配的另一个子串,还要在好后缀的后缀子串中,查找最长的能跟模式串前缀子串匹配的后缀子串。
如果我们只记录刚刚定义的suffix,实际上,只能处理规则的前半部分,也就是,在模式串中,查找跟好后缀匹配的另一个子串。所以,除了suffix数组之外,我们还需要另外一个boolean类型的prefix数组,来记录模式串的后缀子串是否能匹配模式串的前缀子串。

现在,我们来看下,如何来计算并填充这两个数组的值?这个计算过程非常巧妙。
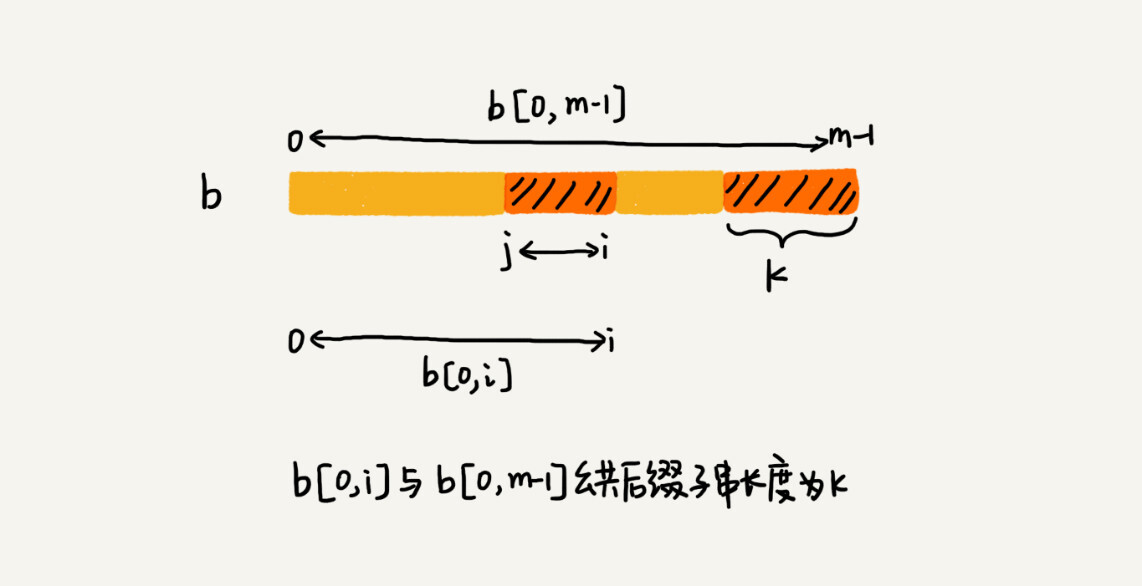
我们拿下标从0到i的子串(i可以是0到m-2)与整个模式串,求公共后缀子串。如果公共后缀子串的长度是k,那我们就记录suffix[k]=j(j表示公共后缀子串的起始下标)。如果j等于0,也就是说,公共后缀子串也是模式串的前缀子串,我们就记录prefix[k]=true。
我们把suffix数组和prefix数组的计算过程,用代码实现出来,就是下面这个样子:
// b表示模式串,m表示长度,suffix,prefix数组事先申请好了
private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {
for (int i = 0; i < m; ++i) { // 初始化
suffix[i] = -1;
prefix[i] = false;
}
for (int i = 0; i < m - 1; ++i) { // b[0, i]
int j = i;
int k = 0; // 公共后缀子串长度
while (j >= 0 && b[j] == b[m-1-k]) { // 与b[0, m-1]求公共后缀子串
--j;
++k;
suffix[k] = j+1; //j+1表示公共后缀子串在b[0, i]中的起始下标
}
if (j == -1) prefix[k] = true; //如果公共后缀子串也是模式串的前缀子串
}
}
有了这两个数组之后,我们现在来看,在模式串跟主串匹配的过程中,遇到不能匹配的字符时,如何根据好后缀规则,计算模式串往后滑动的位数?
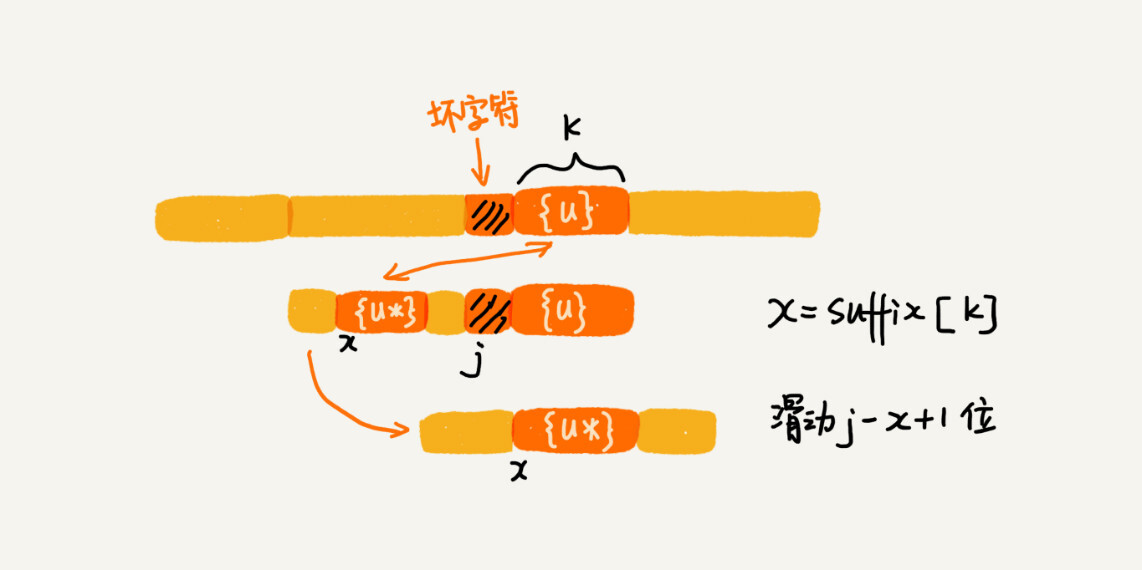
假设好后缀的长度是k。我们先拿好后缀,在suffix数组中查找其匹配的子串。如果suffix[k]不等于-1(-1表示不存在匹配的子串),那我们就将模式串往后移动j-suffix[k]+1位(j表示坏字符对应的模式串中的字符下标)。如果suffix[k]等于-1,表示模式串中不存在另一个跟好后缀匹配的子串片段。我们可以用下面这条规则来处理。
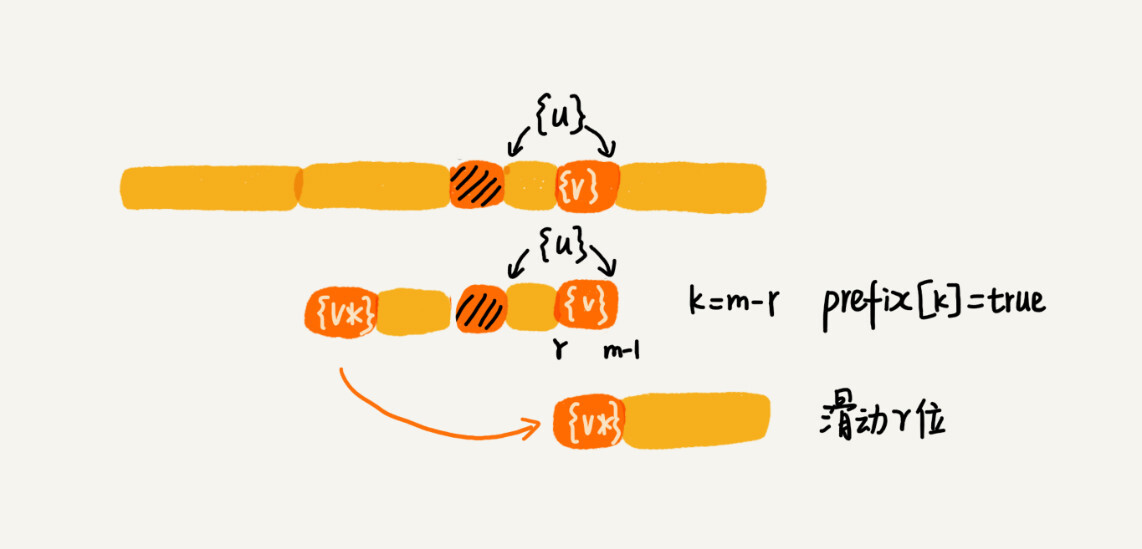
好后缀的后缀子串b[r, m-1](其中,r取值从j+2到m-1)的长度k=m-r,如果prefix[k]等于true,表示长度为k的后缀子串,有可匹配的前缀子串,这样我们可以把模式串后移r位。
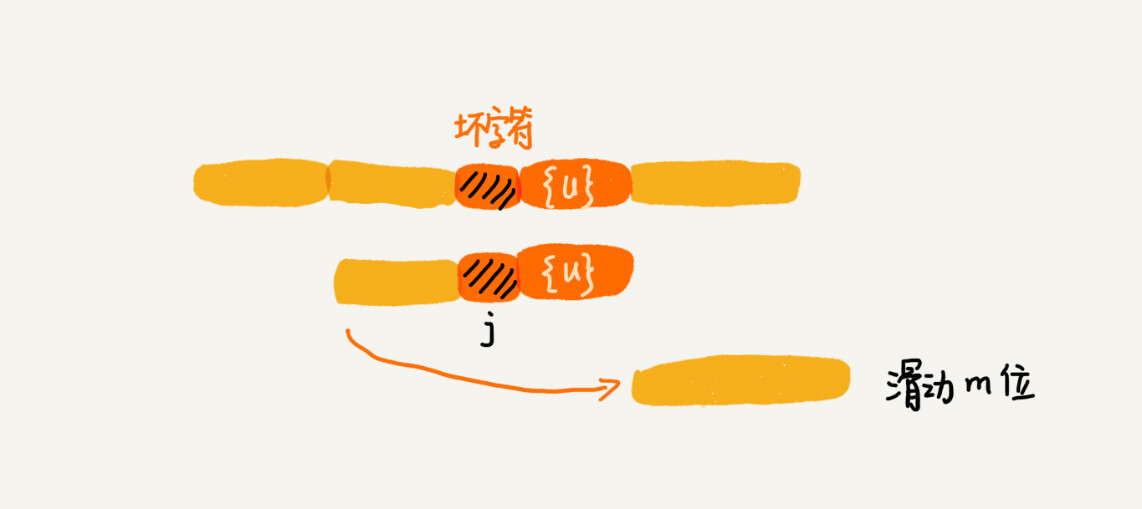
如果两条规则都没有找到可以匹配好后缀及其后缀子串的子串,我们就将整个模式串后移m位。
至此,好后缀规则的代码实现我们也讲完了。我们把好后缀规则加到前面的代码框架里,就可以得到BM算法的完整版代码实现。
// a,b表示主串和模式串;n,m表示主串和模式串的长度。
public int bm(char[] a, int n, char[] b, int m) {
int[] bc = new int[SIZE]; // 记录模式串中每个字符最后出现的位置
generateBC(b, m, bc); // 构建坏字符哈希表
int[] suffix = new int[m];
boolean[] prefix = new boolean[m];
generateGS(b, m, suffix, prefix);
int i = 0; // j表示主串与模式串匹配的第一个字符
while (i <= n - m) {
int j;
for (j = m - 1; j >= 0; --j) { // 模式串从后往前匹配
if (a[i+j] != b[j]) break; // 坏字符对应模式串中的下标是j
}
if (j < 0) {
return i; // 匹配成功,返回主串与模式串第一个匹配的字符的位置
}
int x = j - bc[(int)a[i+j]];
int y = 0;
if (j < m-1) { // 如果有好后缀的话
y = moveByGS(j, m, suffix, prefix);
}
i = i + Math.max(x, y);
}
return -1;
}
// j表示坏字符对应的模式串中的字符下标; m表示模式串长度
private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) {
int k = m - 1 - j; // 好后缀长度
if (suffix[k] != -1) return j - suffix[k] +1;
for (int r = j+2; r <= m-1; ++r) {
if (prefix[m-r] == true) {
return r;
}
}
return m;
}
BM算法的性能分析及优化
我们先来分析BM算法的内存消耗。整个算法用到了额外的3个数组,其中bc数组的大小跟字符集大小有关,suffix数组和prefix数组的大小跟模式串长度m有关。
如果我们处理字符集很大的字符串匹配问题,bc数组对内存的消耗就会比较多。因为好后缀和坏字符规则是独立的,如果我们运行的环境对内存要求苛刻,可以只使用好后缀规则,不使用坏字符规则,这样就可以避免bc数组过多的内存消耗。不过,单纯使用好后缀规则的BM算法效率就会下降一些了。
对于执行效率来说,我们可以先从时间复杂度的角度来分析。
实际上,我前面讲的BM算法是个初级版本。为了让你能更容易理解,有些复杂的优化我没有讲。基于我目前讲的这个版本,在极端情况下,预处理计算suffix数组、prefix数组的性能会比较差。
比如模式串是aaaaaaa这种包含很多重复的字符的模式串,预处理的时间复杂度就是O(m^2)。当然,大部分情况下,时间复杂度不会这么差。关于如何优化这种极端情况下的时间复杂度退化,如果感兴趣,你可以自己研究一下。
实际上,BM算法的时间复杂度分析起来是非常复杂,这篇论文“A new proof of the linearity of the Boyer-Moore string searching algorithm”证明了在最坏情况下,BM算法的比较次数上限是5n。这篇论文“Tight bounds on the complexity of the Boyer-Moore string matching algorithm”证明了在最坏情况下,BM算法的比较次数上限是3n。你可以自己阅读看看。
解答开篇&内容小结
今天,我们讲了一种比较复杂的字符串匹配算法,BM算法。尽管复杂、难懂,但匹配的效率却很高,在实际的软件开发中,特别是一些文本编辑器中,应用比较多。如果一遍看不懂的话,你就多看几遍。
BM算法核心思想是,利用模式串本身的特点,在模式串中某个字符与主串不能匹配的时候,将模式串往后多滑动几位,以此来减少不必要的字符比较,提高匹配的效率。BM算法构建的规则有两类,坏字符规则和好后缀规则。好后缀规则可以独立于坏字符规则使用。因为坏字符规则的实现比较耗内存,为了节省内存,我们可以只用好后缀规则来实现BM算法。
课后思考
你熟悉的编程语言中的查找函数,或者工具、软件中的查找功能,都是用了哪种字符串匹配算法呢?
欢迎留言和我分享,也欢迎点击“请朋友读”,把今天的内容分享给你的好友,和他一起讨论、学习。