11 KiB
上一讲中我给你讲了数据集成,今天我来讲下数据变换。
如果一个人在百分制的考试中得了95分,你肯定会认为他学习成绩很好,如果得了65分,就会觉得他成绩不好。如果得了80分呢?你会觉得他成绩中等,因为在班级里这属于大部分人的情况。
为什么会有这样的认知呢?这是因为我们从小到大的考试成绩基本上都会满足正态分布的情况。什么是正态分布呢?正态分布也叫作常态分布,就是正常的状态下,呈现的分布情况。
比如你可能会问班里的考试成绩是怎样的?这里其实指的是大部分同学的成绩如何。以下图为例,在正态分布中,大部分人的成绩会集中在中间的区域,少部分人处于两头的位置。正态分布的另一个好处就是,如果你知道了自己的成绩,和整体的正态分布情况,就可以知道自己的成绩在全班中的位置。
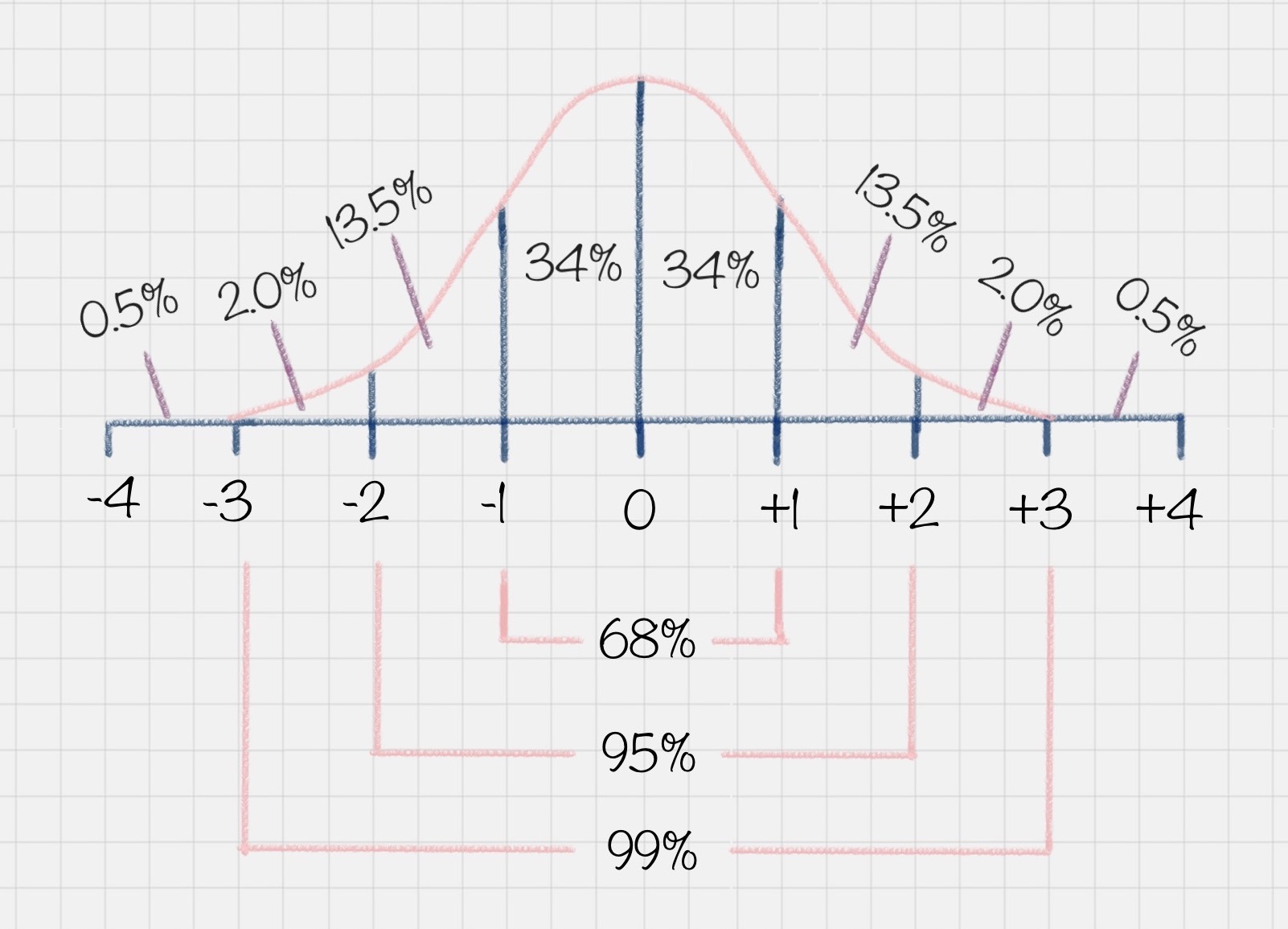
另一个典型的例子就是,美国SAT考试成绩也符合正态分布。而且美国本科的申请,需要中国高中生的GPA在80分以上(百分制的成绩),背后的理由也是默认考试成绩属于正态分布的情况。
为了让成绩符合正态分布,出题老师是怎么做的呢?他们通常可以把考题分成三类:
第一类:基础题,占总分70%,基本上属于送分题;
第二类:灵活题,基础范围内+一定的灵活性,占20%;
第三类:难题,涉及知识面较广的难题,占10%;
那么,你想下,如果一个出题老师没有按照上面的标准来出题,而是将第三类难题比重占到了70%,也就是我们说的“超纲”,结果会是怎样呢?
你会发现,大部分人成绩都“不及格”,最后在大家激烈的讨论声中,老师会将考试成绩做规范化处理,从而让成绩满足正态分布的情况。因为只有这样,成绩才更具有比较性。所以正态分布的成绩,不仅可以让你了解全班整体的情况,还能了解每个人的成绩在全班中的位置。
数据变换在数据分析中的角色
我们再来举个例子,假设A考了80分,B也考了80分,但前者是百分制,后者500分是满分,如果我们把从这两个渠道收集上来的数据进行集成、挖掘,就算使用效率再高的算法,结果也不是正确的。因为这两个渠道的分数代表的含义完全不同。
所以说,有时候数据变换比算法选择更重要,数据错了,算法再正确也是错的。你现在可以理解为什么80%的工作时间会花在前期的数据准备上了吧。
那么如何让不同渠道的数据统一到一个目标数据库里呢?这样就用到了数据变换。
在数据变换前,我们需要先对字段进行筛选,然后对数据进行探索和相关性分析,接着是选择算法模型(这里暂时不需要进行模型计算),然后针对算法模型对数据的需求进行数据变换,从而完成数据挖掘前的准备工作。
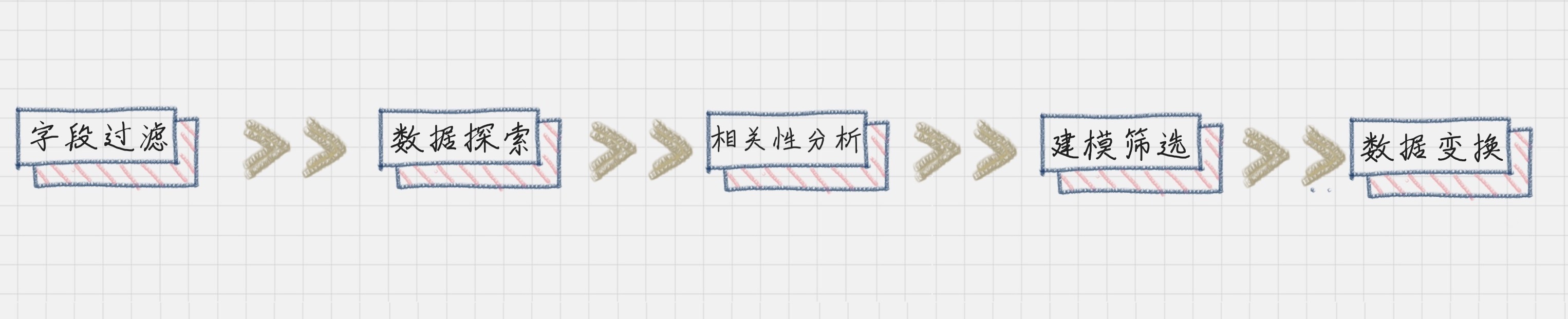
所以你从整个流程中可以看出,数据变换是数据准备的重要环节,它通过数据平滑、数据聚集、数据概化和规范化等方式将数据转换成适用于数据挖掘的形式。
我来介绍下这些常见的变换方法:
在这些变换方法中,最简单易用的就是对数据进行规范化处理。下面我来给你讲下如何对数据进行规范化处理。
数据规范化的几种方法
1. Min-max 规范化
Min-max规范化方法是将原始数据变换到[0,1]的空间中。用公式表示就是:
新数值=(原数值-极小值)/(极大值-极小值)。
2. Z-Score 规范化
假设A与B的考试成绩都为80分,A的考卷满分是100分(及格60分),B的考卷满分是500分(及格300分)。虽然两个人都考了80分,但是A的80分与B的80分代表完全不同的含义。
那么如何用相同的标准来比较A与B的成绩呢?Z-Score就是用来可以解决这一问题的。
我们定义:新数值=(原数值-均值)/ 标准差。
假设A所在的班级平均分为80,标准差为10。B所在的班级平均分为400,标准差为100。那么A的新数值=(80-80)/10=0,B的新数值=(80-400)/100=-3.2。
那么在Z-Score标准下,A的成绩会比B的成绩好。
我们能看到Z-Score的优点是算法简单,不受数据量级影响,结果易于比较。不足在于,它需要数据整体的平均值和方差,而且结果没有实际意义,只是用于比较。
3.小数定标规范化
小数定标规范化就是通过移动小数点的位置来进行规范化。小数点移动多少位取决于属性A的取值中的最大绝对值。
举个例子,比如属性A的取值范围是-999到88,那么最大绝对值为999,小数点就会移动3位,即新数值=原数值/1000。那么A的取值范围就被规范化为-0.999到0.088。
上面这三种是数值规范化中常用的几种方式。
Python的SciKit-Learn库使用
SciKit-Learn是Python的重要机器学习库,它帮我们封装了大量的机器学习算法,比如分类、聚类、回归、降维等。此外,它还包括了数据变换模块。
我现在来讲下如何使用SciKit-Learn进行数据规范化。
1. Min-max 规范化
我们可以让原始数据投射到指定的空间[min, max],在SciKit-Learn里有个函数MinMaxScaler是专门做这个的,它允许我们给定一个最大值与最小值,然后将原数据投射到[min, max]中。默认情况下[min,max]是[0,1],也就是把原始数据投放到[0,1]范围内。
我们来看下下面这个例子:
# coding:utf-8
from sklearn import preprocessing
import numpy as np
# 初始化数据,每一行表示一个样本,每一列表示一个特征
x = np.array([[ 0., -3., 1.],
[ 3., 1., 2.],
[ 0., 1., -1.]])
# 将数据进行[0,1]规范化
min_max_scaler = preprocessing.MinMaxScaler()
minmax_x = min_max_scaler.fit_transform(x)
print minmax_x
运行结果:
[[0. 0. 0.66666667]
[1. 1. 1. ]
[0. 1. 0. ]]
2. Z-Score规范化
在SciKit-Learn库中使用preprocessing.scale()函数,可以直接将给定数据进行Z-Score规范化。
from sklearn import preprocessing
import numpy as np
# 初始化数据
x = np.array([[ 0., -3., 1.],
[ 3., 1., 2.],
[ 0., 1., -1.]])
# 将数据进行Z-Score规范化
scaled_x = preprocessing.scale(x)
print scaled_x
运行结果:
[[-0.70710678 -1.41421356 0.26726124]
[ 1.41421356 0.70710678 1.06904497]
[-0.70710678 0.70710678 -1.33630621]]
这个结果实际上就是将每行每列的值减去了平均值,再除以方差的结果。
我们看到Z-Score规范化将数据集进行了规范化,数值都符合均值为0,方差为1的正态分布。
3. 小数定标规范化
我们需要用NumPy库来计算小数点的位数。NumPy库我们之前提到过。
这里我们看下运行代码:
# coding:utf-8
from sklearn import preprocessing
import numpy as np
# 初始化数据
x = np.array([[ 0., -3., 1.],
[ 3., 1., 2.],
[ 0., 1., -1.]])
# 小数定标规范化
j = np.ceil(np.log10(np.max(abs(x))))
scaled_x = x/(10**j)
print scaled_x
运行结果:
[[ 0. -0.3 0.1]
[ 0.3 0.1 0.2]
[ 0. 0.1 -0.1]]
数据挖掘中数据变换比算法选择更重要
在考试成绩中,我们都需要让数据满足一定的规律,达到规范性的要求,便于进行挖掘。这就是数据变换的作用。
如果不进行变换的话,要不就是维数过多,增加了计算的成本,要不就是数据过于集中,很难找到数据之间的特征。
在数据变换中,重点是如何将数值进行规范化,有三种常用的规范方法,分别是Min-Max规范化、Z-Score规范化、小数定标规范化。其中Z-Score规范化可以直接将数据转化为正态分布的情况,当然不是所有自然界的数据都需要正态分布,我们也可以根据实际的情况进行设计,比如取对数log,或者神经网络里采用的激励函数等。

在最后我给大家推荐了Python的sklearn库,它和NumPy, Pandas都是非常有名的Python库,在数据统计工作中起了很大的作用。SciKit-Learn不仅可以用于数据变换,它还提供了分类、聚类、预测等数据挖掘算法的API封装。后面我会详细给你讲解这些算法,也会教你如何使用SciKit-Learn工具来完成数据挖掘算法的工作。
最后给你留道思考题吧,假设属性income的最小值和最大值分别是5000元和58000元。利用Min-Max规范化的方法将属性的值映射到0至1的范围内,那么属性income的16000元将被转化为多少?
另外数据规范化都有哪些方式,他们是如何进行规范化的?欢迎在评论区与我分享你的答案,也欢迎你把这篇文章分享给你的朋友或者同事,一起讨论一下。